ТЕОРЕМА 13.1.15. (Чебышева). Если 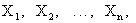– попарно независимые случайные величины, причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало ни было положительное число 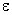, вероятность неравенства

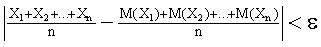
будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами,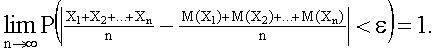

Таким образом, теорема Чебышева утверждает, что если рассматривается достаточно большое число независимых случайных величин, имеющих ограниченные дисперсии, то почти достоверным можно считать событие, состоящее в том, что отклонение среднего арифметического случайных величин от среднего арифметического их математических ожиданий будет по абсолютной величине сколь угодно малым.

Доказательство. Введем в рассмотрение новую случайную величину – среднее арифметическое случайных величин

.

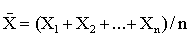Найдем математическое ожидание 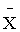. Пользуясь свойствами математического ожидания (постоянный множитель можно вынести за знак математического ожидания, математическое ожидание суммы равно сумме математических ожиданий слагаемых), получим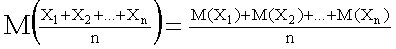
. (13.1.38)

Применяя к величине неравенство Чебышева, имеем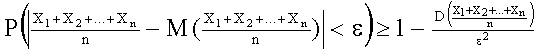

или, учитывая соотношение (13.1.38), получим: 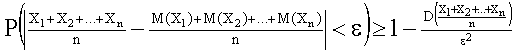(13.1.39).

Пользуясь свойствами дисперсии (постоянный множитель можно вынести за знак дисперсии, возведя его в квадрат; дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых), получим .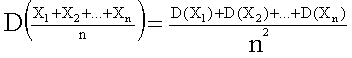

По условию дисперсии всех случайных величин ограничены постоянным числом С, т. е. имеют место неравенства:
.

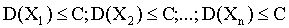Поэтому .

Итак, 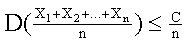. (13.1.40)

Подставляя правую часть (13.1.40) в неравенство (13.1.39) (отчего последнее может быть лишь усилено), имеем
.

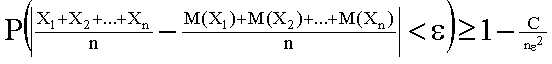Отсюда, переходя к пределу при 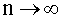, получим

.

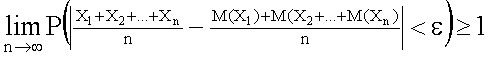Наконец, учитывая, что вероятность не может превышать единицу, окончательно можем написать
.
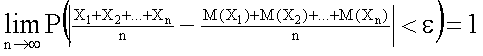Теорема доказана.

При формулировке теоремы Чебышева предполагалось, что случайные величины имеют различные математические ожидания. На практике часто бывает, что случайные величины имеют одно и то же математическое ожидание. Если вновь допустить, что дисперсии этих величин ограничены, то к ним будет применима теорема Чебышева.

Пусть а — математическое ожидание каждой из случайных величин. В рассматриваемом случае среднее арифметическое математических ожиданий, как легко видеть, также равно а. Для рассматриваемого частного случая теорема Чебышева формулируется следующим образом.

Если 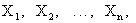– попарно независимые случайные величины, имеющие одно и то же математическое ожидание а, и если дисперсии этих величин равномерно ограничены, то, как бы мало ни было положительное число 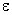, вероятность неравенства

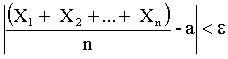
будет как угодно близка к единице, если число случайных величин достаточно велико.

Другими словами, будет иметь место равенство

.

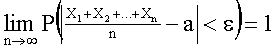Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >