Рассмотрим дискретную случайную величину X, заданную законом распределения:
| X | 1 | 10 | 20 | 150 |
| p | 0,2 | 0,4 | 0,3 | 0,1 |
Найдем математическое ожидание M(X):
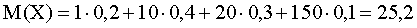
Напишем закон распределения случайной величины :
 |
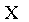1 | 100 | 400 | 22500 |
| p | 0,2 | 0,4 | 0,3 | 0,1 |
Найдем математическое ожидание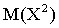 
:
.
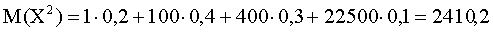Видим, что 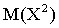: значительно больше M(X) . Это объясняется тем, что после возведения в квадрат возможное значение величины 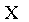, соответствующее значению х=150 величины X, стало равным 22500, т. е. значительно увеличилось; вероятность же этого значения мала (0,1).
Таким образом, переход от M(X) к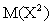 
позволил лучше учесть влияние на математическое ожидание того возможного значения, которое велико и имеет малую вероятность. Разумеется, если бы величина Х имела несколько больших и маловероятных значений, то переход к величине 
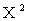, а тем более к величинам 
, 
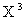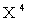и т. д., позволил бы еще больше “усилить роль” этих больших, но маловероятных возможных значений. Вот почему оказывается целесообразным рассматривать математическое ожидание целой положительной степени случайной величины (не только дискретной, но и непрерывной).
Начальным моментом порядка k случайной величины Х называют математическое ожидание величины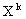 
:
.
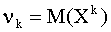В частности,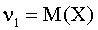 
, 
.
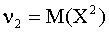Пользуясь этими моментами, формулу для вычисления дисперсии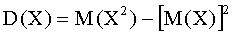 
можно записать так:
.
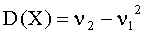Кроме моментов случайной величины Х, целесообразно рассматривать моменты отклонений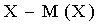 
.
Центральным моментом порядка k случайной величины Х называют математическое ожидание величины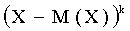 
:
.
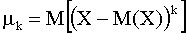В частности,
,
.
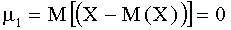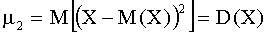Легко выводятся соотношения, связывающие начальные и центральные моменты. Например, сравнивая выражения для дисперсии, получим
.
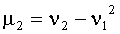Нетрудно, исходя из определения центрального момента и пользуясь свойствами математического ожидания, получить формулы
,
.
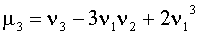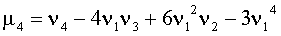Моменты более высоких порядков применяются редко.
Отметим, что моменты, рассмотренные здесь, называют теоретическими. В отличие от теоретических моментов моменты, которые вычисляются по данным наблюдений, называют эмпирическими.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
