Случайное событие определяется как событие, которое при осуществлении определенного комплекса условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S не налагается, то такую вероятность называют безусловной, если же налагаются другие дополнительные условия, то вероятность называют условной. Например, часто приходится вычислять вероятность одного события при дополнительном условии, что произошло другое событие.

Пусть А и В – наблюдаемые события в испытании.

Условной вероятностью Р(В/А) наступления события В при условии, что событие А произошло в результате испытания, называется величина определяемая равенством 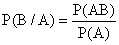. (13.1.10)

Аналогично определяется условная вероятность Р(А/В)

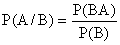, где Р(А)>0, P(B)>0. (13.1.11)

Основанием для подобного введения условной вероятности служит свойство 5, справедливое для статистического и классического определения вероятности.

ПРИМЕР 13.1.12 В урне 3 белых и 2 красных шара. Из урны последовательно без возвращения извлекают два шара (испытание). Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен красный шар (событие А).

Решение. После первого испытания, когда произошло событие А, в урне осталось 4 шара, из них 3 белых.

Искомая условная вероятность равна .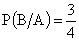

Определим теперь 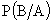по формуле (13.1.10).

Вероятность появления красного шара в первом испытании .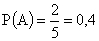

Найдем вероятность 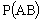того, что в первом испытании извлечен красный шар, а затем – белый. Общее число случаев совместного появления двух шаров любого цвета .

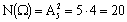При этом событию 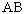случаев.

Следовательно, .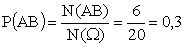

По формуле (13.1.10)

.

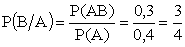Как и следовало ожидать, ответ получился такой же, как и при непосредственном вычислении.

Теоремы умножения вероятностей

Из формул (13.1.10), (13.1.11) получается теорема умножения вероятностей для зависимых событий. Случайные события называются зависимыми, если вероятность наступления одного из них зависит от того, имело место или нет другое событие. Если для примера 13.1.12 в первом испытании наступило бы событие А (извлечен не красный, а белый шар), то

.

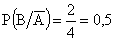Следовательно, событие В зависит от события А.

ТЕОРЕМА 13.1.1 Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило.
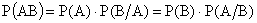. (13.1.12)

ПРИМЕР 13.1.13 Вероятность попадания ракеты в цель (событие А) 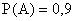. Вероятность поражения цели при попадании в нее одной ракеты (событие В) 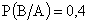. Найти вероятность поражения цели при пуске одной ракеты.

Решение. Событие АВ – ракета попала в цель и цель поражена.

По теореме 13.1.1: .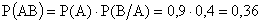

Теорему 13.1.1 можно обобщить на случай любого числа событий.

ТЕОРЕМА 13.1.2 Вероятность произведения нескольких событий равна произведению вероятности одного из них на условные вероятности остальных событий, причем вероятность каждого последующего события вычисляется в предположении, что предыдущие события уже наступили.

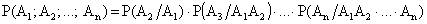.(13.1.13)

В частности, для трех событий:

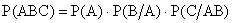. (13.1.14)

Событие А называется независимым от события B, если выполняется условие
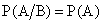, где 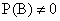. (13.1.15)

Если событие А не зависит от события В, то и событие В не зависит от события А, что следует из формулы (13.1.13) с учетом формулы (13.1.15): 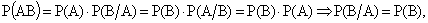(13.1.16)

где .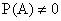

Это означает, что свойство независимости событий взаимно.

События А и В называются независимыми, если 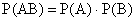. (13.1.17)

Формула (13.1.17) выражает теорему умножения для независимых событий.

Теорема 13.1.3 Вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

События 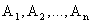называются независимыми в совокупности, если для любого набора из 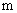событий 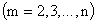выполняется равенство:
.

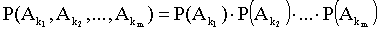ТЕОРЕМА 13.1.4 Вероятность произведения нескольких независимых в совокупности событий равна произведению вероятностей этих событий: 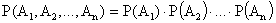. (13.1.18)

Независимость событий

Формулы (13.1.17), (13.1.18) позволяют установить независимость (зависимость) событий, если известны вероятности всех нужных событий. На практике независимость событий обычно устанавливают из физических соображений.

ПРИМЕР 13.1.14 Два стрелка производят по одному выстрелу по цели. Вероятность попадания в цель для первого стрелка (событие А1) 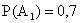, вероятность попадания в цель для второго стрелка (событие А2) .

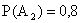Чему равна вероятность того, что оба стрелка попадут в цель?

Решение. События 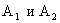— независимы.
.

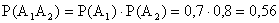Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >