Пусть непрерывная случайная величина Х распределена по показательному закону
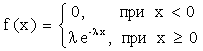 .
.
Найдем математическое ожидание: 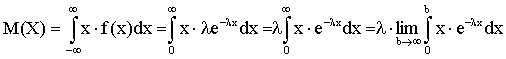
.
Производя интегрирование по частям, и находя предел, получим
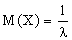 .
.
Таким образом, математическое ожидание показательного распределения равно обратной величине параметра.
Найдем дисперсию:
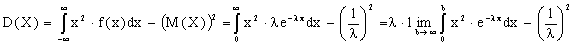 .
.
Дважды интегрируя по частям, и находя предел, получаем
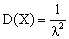 .
.
Найдем среднее квадратическое отклонение: 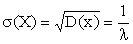
Сравнивая 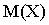 и
и 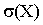 , получаем
, получаем
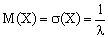 ,
,
т. е. математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
ПРИМЕР 13.1.36 Непрерывная случайная величина Х распределена по показательному закону 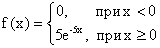
Найти математическое ожидание, среднее квадратическое отклонение и дисперсию X.
Решение. По условию, 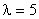 . Следовательно,
. Следовательно,
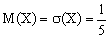 ,
, 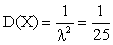 .
.
Показательное распределение широко применяется в приложениях, в частности, в теории надежности, теории массового обслуживания, в физике, биологии и др.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >