Комбинаторика изучает количества комбинаций (наборов), подчиненных определенным условиям, которые можно составить из элементов заданного конечного множества. При непосредственном вычислении вероятностей формулы комбинаторики часто используются. Из конечного множества 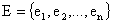, состоящего из n различных элементов, можно образовывать различные наборы, состоящие из m 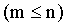элементов.

Перестановками из n различных элементов называются наборы, содержащие по n элементов и отличающиеся только порядком их расположения (упорядоченные наборы без повторений из n элементов по n). Число всех таких перестановок обозначают Р и определяют по формуле

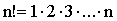(n — факториал). (13.1.3)

Конечное множество называется упорядоченным, если его элементы перенумерованы некоторым образом. Каждое упорядочение заключается в том, что какой-то элемент получает номер 1, какой-то – номер 2, …, какой-то номер – n. Номер 1 может получить любой элемент множества Е; значит, выбор первого элемента можно произвести n способами. Если первый элемент выбран, то на второе место остается лишь (n-1) кандидат, так как повторить сделанный выбор нельзя. Третий элемент можно выбрать (n-2) способами и т.д. Последний элемент можно выбрать лишь одним способом, он и займет n-е место. Общее число способов упорядочения равно:

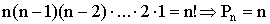
Здесь мы воспользовались правилом произведения: если элемент х можно выбрать m способами, а элемент y можно выбрать n способами, то упорядоченную пару (х,у) можно выбрать 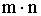способами.

ПРИМЕР 13.1.3 Сколькими способами можно три фотографии на выставке повесить в один ряд?

Решение. Искомое число: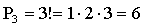

Проиллюстрируем данный пример

Размещениями называются наборы из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком (упорядоченные наборы без повторений из n элементов по m). Число всех размещений равно:

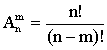(13.1.4)

ПРИМЕР 13.1.4 В урне 7 шаров разного цвета. Из них наудачу отбирают 2 шара и раскладывают по лункам №1 и №2. Сколько вариантов распределения шаров по лункам существует?

Решение. В данном случае повтора элементов нет, порядок — есть. Искомое число: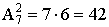

Сочетаниями называются наборы, составленные из n различных элементов по m (неупорядоченные наборы без повторений из n элементов по m). Их число обозначается 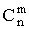. Так как каждый набор можно упорядочить 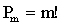способами, то имеем 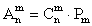, откуда получаем

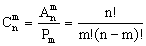(13.1.5)

ПРИМЕР 13.1.5 Сколькими способами из 6 студентов можно отобрать для участия в соревнованиях 2 студентов?

Решение.

В данном случае повтора нет (одного студента дважды отобрать нельзя), порядок — неважен. Тогда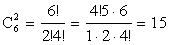

Для чисел 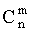, называемых также биномиальными коэффициентами, справедливы следующие тождества, часто оказывающиеся полезными при решении задач.

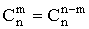1. (свойства симметрии)
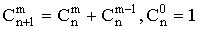2. (рекуррентное соотношение)
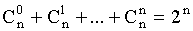3. (следствие бинома Ньютона).

Если выбор m элементов из n различных элементов производится с возвращением (отобранный элемент возвращается в исходное множество и может быть снова выбран – схема выбора с возвращением) и с упорядочиванием, то различные наборы будут с повторениями, отличаясь либо составом элементов, либо порядком их следования. Получаемые в результате комбинации называются размещениями с повторениями, а их общее число определяется формулой

(13.1.6)

Если среди n элементов есть 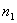элементов одного вида, 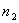элементов другого вида и т.д., то число перестановок с повторениями определяются формулой 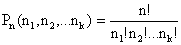(13.1.7)

где .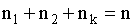

Число сочетаний с повторениями из n элементов по m равно числу сочетаний без повторений из n+m-1 элементов по m элементов, т.е.

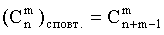.(13.1.8)

При решении задач комбинаторики используют следующие правила.

Правило суммы. Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m+n способами.

Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана 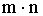способами.

ПРИМЕР 13.1.6 Кодовый замок имеет пять дисков, посаженных на одну ось. Каждый диск разбит на сектора с номерами 1, 2, 3, 4. Замок открывается при установке одной определенной комбинации цифр. Найти вероятность того, что в результате набора наугад цифровой комбинации в окне замка он откроется.

Решение. Имеем схему урн. Общее число случаев равно числу размещений с повторениями из 4 элементов по 5, т.е. .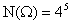

Пусть событие А – замок открылся. Этому событию благоприятен лишь один случай N(A)=1.

Поэтому .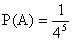

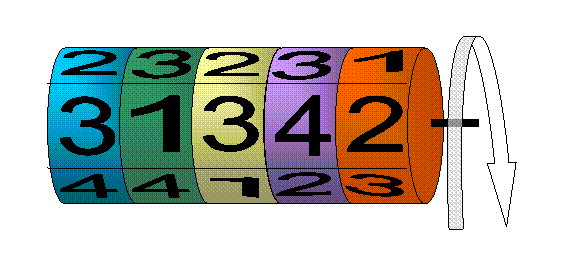
ПРИМЕР 13.1.7 Сколько различных шестизначных чисел можно записать с помощью цифр 1; 1; 1; 2; 2; 2?

Решение. Здесь нужно найти число перестановок с повторениями, которое определяется формулой (13.1.7). При k=2, 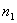=3, 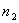=3, n=6 по формуле получаем .

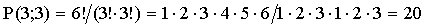ПРИМЕР 13.1.8 Из букв слова РОТОР, составленного с помощью разрезной азбуки, наудачу последовательно извлекают 3 буквы и складывают в ряд. Какова вероятность того, что получится слово ТОР?

Решение. Чтобы отличить одинаковые буквы друг от друга, снабдим их номерами:.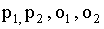

Общее число случаев равно: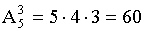

Слово “тор” получится в случаях .

Искомая вероятность равна Р=4/60=1/15.

При подсчете числа благоприятных случаев воспользовались правилом произведения: букву “т” можно выбрать одним способом, букву “о” – двумя, букву “р” – двумя способами.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >