1. Уравнение, не содержащее искомой функции 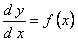 , в предположении, что его правая часть непрерывна в интервале
, в предположении, что его правая часть непрерывна в интервале  , интегрируется в квадратурах. Его общее решение будет
, интегрируется в квадратурах. Его общее решение будет
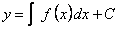 .
.
ПРИМЕР 11.1.6 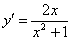 , тогда
, тогда 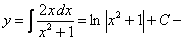 общее решение.
общее решение.
ПРИМЕР 11.1.7 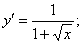
Решение.
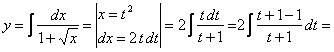
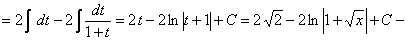 общее решение.
общее решение.
2. Уравнения, не содержащие независимой переменной
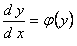 ,
,
где 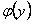 определена и непрерывна в интервале
определена и непрерывна в интервале  и не обращается в этом
и не обращается в этом
интервале в нуль. Тогда данное уравнение равносильно уравнению 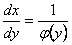 ; общее решение имеет вид
; общее решение имеет вид 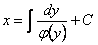 .
.
ПРИМЕР 11.1.8 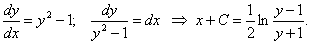
ПРИМЕР 11.1.9 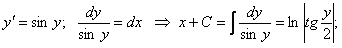 итак, общий интеграл уравнения имеет вид
итак, общий интеграл уравнения имеет вид  .
.
3. Уравнения с разделенными переменными 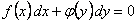 . В каждом
. В каждом 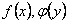 суть функции, зависящие соответственно только от
суть функции, зависящие соответственно только от 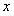 и только от
и только от 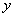 , и непрерывная при рассматриваемых значениях
, и непрерывная при рассматриваемых значениях 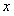 и
и 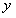 . Это уравнение интегрируется непосредственно: равенство
. Это уравнение интегрируется непосредственно: равенство 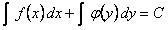 является общим интегралом уравнения.
является общим интегралом уравнения.
ПРИМЕР 11.1.10 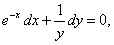
Решение.
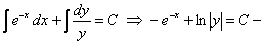 общий интеграл данного уравнения.
общий интеграл данного уравнения.
4. Уравнения с разделяющимися переменными
Уравнение вида 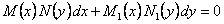 , в котором коэффициенты при
, в котором коэффициенты при 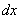 и
и 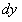 являются произведениями функций, зависящих только от одной из переменных
являются произведениями функций, зависящих только от одной из переменных 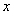 и
и 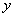 , называется уравнением с разделяющимися переменными.
, называется уравнением с разделяющимися переменными.
Предположим, что функции 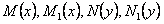 непрерывны при рассматриваемых значениях
непрерывны при рассматриваемых значениях 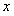 и
и 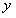 . Тогда, умножая обе части уравнения на
. Тогда, умножая обе части уравнения на 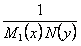
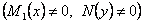 , получаем уравнение с разделяющимися переменными
, получаем уравнение с разделяющимися переменными
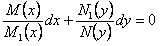 .
.
Поэтому общий интеграл уравнения будет 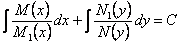 .
.
ПРИМЕР 11.1.11 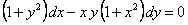
Решение.
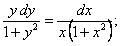
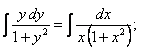
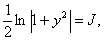
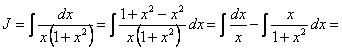
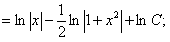
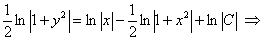
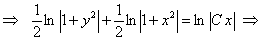
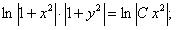
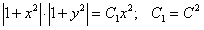 .
.
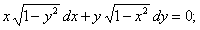
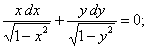
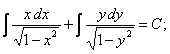
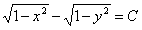 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >