Уравнение вида

,

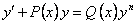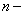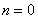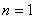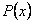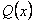где любое число, отличное от нуля и единицы, называется уравнением Бернулли (при или при уравнение Бернулли обращается в линейное уравнение). Будем предполагать, что функции и определены и непрерывны в некотором интервале.

Уравнение Бернулли всегда интегрируется в квадратурах, ибо оно делением обеих частей на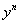 и подстановкой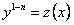, где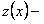 новая искомая функция, приводится к линейному уравнению. В самом деле, разделив обе части на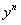, получим.

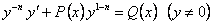Сделаем подстановку;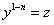

;

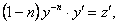
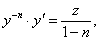
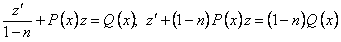если обозначим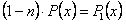 и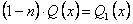, то получим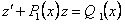. Интегрируя это уравнение, находим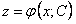. Возвращаясь к нашей подстановке, находим.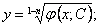

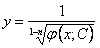Вышесказанное продемонстрируем на примере. Разделив обе части на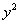, получим.

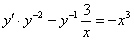Сделаем подстановку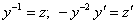. Подставляя в уравнение, получим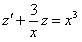. Это линейное неоднородное уравнение относительно искомой функции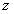. Решим это уравнение, применяя готовую формулу

.

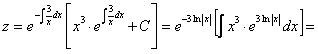
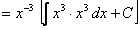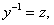Итак, но то

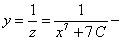общее решение уравнения Бернулли.

Замечание. Уравнение Бернулли можно проинтегрировать методом подстановки.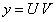

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >