Известно, что полный дифференциал функции 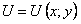 имеет вид
имеет вид 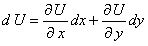 .
.
Рассмотрим дифференциальное уравнение первого порядка в симметричной форме
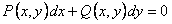 .(11.1.13)
.(11.1.13)
Если бы оказалось, что левая часть этого уравнения представляет полный дифференциал некоторой функции 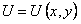 , в этом случае дифференциальное уравнение называют уравнением в полных дифференциалах
, в этом случае дифференциальное уравнение называют уравнением в полных дифференциалах
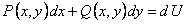 , то зная функцию
, то зная функцию 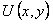 получили бы общий интеграл уравнения в виде
получили бы общий интеграл уравнения в виде 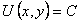 .
.
Возникает вопрос, как установить, является ли дифференциальное выражение 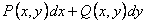 полным дифференциалом некоторой функции; если это так, то как найти эту функцию.
полным дифференциалом некоторой функции; если это так, то как найти эту функцию.
На этот вопрос отвечает следующая теорема.
ТЕОРЕМА 11.1.2 Пусть функции 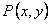 и
и 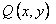 определены и непрерывны в некоторой области и имеют в ней непрерывные частные производные
определены и непрерывны в некоторой области и имеют в ней непрерывные частные производные 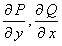 . Тогда для того, чтобы дифференциальное выражение
. Тогда для того, чтобы дифференциальное выражение 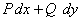 представляло собой полный дифференциал некоторой функции
представляло собой полный дифференциал некоторой функции 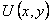 , необходимо и достаточно, чтобы во всех точках области
, необходимо и достаточно, чтобы во всех точках области 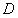 было
было
выполнено условие 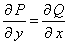 .
.
Доказательство этой теоремы опускаем.
Тогда функция 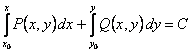 является общим интегралом дифференциального уравнения.
является общим интегралом дифференциального уравнения.
ПРИМЕР 11.1.16 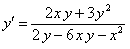 .
.
Решение.
Это уравнение не является ни уравнением с разделяющимися переменными, ни однородным, ни линейным. Написав его в симметрическом виде  и убедившись, что
и убедившись, что 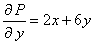 ,
, 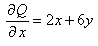 , так как
, так как 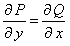 , заключаем, что данное уравнение – в полных дифференциалах. Общий интеграл его находим по формуле,
, заключаем, что данное уравнение – в полных дифференциалах. Общий интеграл его находим по формуле,
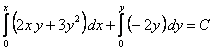 ,
, 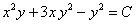 .
.
При интегрировании уравнения в полных дифференциалах можно обойтись без готовой формулы, а искать функцию 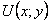 постепенно, пользуясь знанием ее частных производных
постепенно, пользуясь знанием ее частных производных 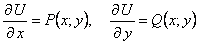 .
.
Из первого равенства 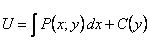 .
.
Функцию 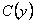 далее подбираем так, чтобы удовлетворить и второму условию
далее подбираем так, чтобы удовлетворить и второму условию 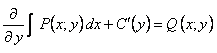 . Из этого находим
. Из этого находим 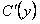 , а по нему и
, а по нему и 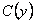 .
.
ПРИМЕР 11.1.17 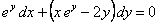 .
.
Решение.
Это уравнение в полных дифференциалах, так как 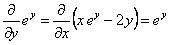 .
.
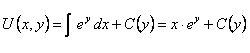 .
.
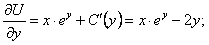

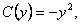 следовательно,
следовательно, 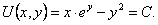
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >