ОПРЕДЕЛЕНИЕ 11.2.7 Дифференциальное уравнение 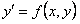 называется уравнением с разделяющимися переменными, если его правая часть есть произведение двух функций, одна из которых зависит от
называется уравнением с разделяющимися переменными, если его правая часть есть произведение двух функций, одна из которых зависит от 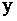 , а другая от
, а другая от 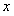 .
. 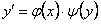 .
.
Предположим, что функции 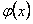 и
и 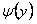 непрерывны на интервале
непрерывны на интервале 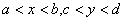 и что
и что 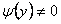 .
.
Умножая обе части уравнения 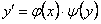 на
на 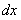 и деля на
и деля на 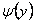 , запишем его в виде:
, запишем его в виде: 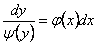 .
.
Почленное интегрирование последнего уравнения приводит к соотношению 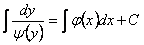 , которое представляет собой общий интеграл данного уравнения в указанной области.
, которое представляет собой общий интеграл данного уравнения в указанной области.
ОПРЕДЕЛЕНИЕ 11.2.8 Дифференциальное уравнение
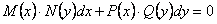 называется дифференциальным уравнением с разделяющимися переменными в симметричной относительно
называется дифференциальным уравнением с разделяющимися переменными в симметричной относительно 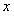 и
и 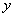 дифференциальной форме.
дифференциальной форме.
Функции 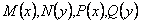 непрерывны соответственно в интервалах
непрерывны соответственно в интервалах 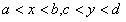 и не равны тождественно нулю.
и не равны тождественно нулю.
Для нахождения всех решений такого уравнения достаточно разделить обе части уравнения на произведение 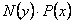 и проинтегрировать полученное соотношение:
и проинтегрировать полученное соотношение: 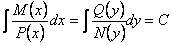 . Полученное соотношение является общим интегралом данного уравнения, где
. Полученное соотношение является общим интегралом данного уравнения, где 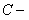 произвольная постоянная.
произвольная постоянная.
ОПРЕДЕЛЕНИЕ 11.2.9 Уравнение вида 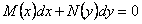 называется дифференциальным уравнением с разделенными переменными.
называется дифференциальным уравнением с разделенными переменными.
Почленное интегрирование данного уравнения приводит к соотношению 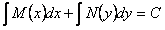 , которое определяет (в неявной форме) решение исходного уравнения.
, которое определяет (в неявной форме) решение исходного уравнения.
ПРИМЕР 11.2.1. Найти общее решение уравнения 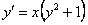 .
.
Решение.
Данное уравнение есть уравнение с разделяющимися переменными 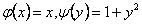 функции
функции 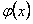 и
и 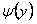 непрерывна всюду и
непрерывна всюду и  .
.
Разделяя переменными и интегрируя , получим
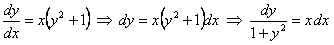
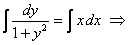
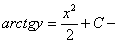 общий интеграл данного уравнения во всей плоскости
общий интеграл данного уравнения во всей плоскости 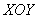 .
.
Разрешая относительно  , находим общее решение
, находим общее решение 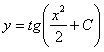 ,
, 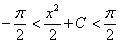 .
.
ПРИМЕР 11.2.2. Найти общий интеграл уравнения
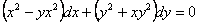 .
.
Решение.
Преобразуем данное уравнение
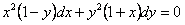 . Данное уравнение есть уравнение с разделяющимися переменными в дифференциальной форме симметричное относительно
. Данное уравнение есть уравнение с разделяющимися переменными в дифференциальной форме симметричное относительно 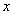 и
и 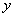 .
.
Функции 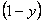 и
и 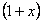 не равны нулю в рассматриваемой области. Разделим обе части уравнения на
не равны нулю в рассматриваемой области. Разделим обе части уравнения на 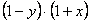 , получим
, получим
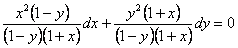
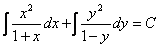
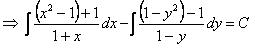
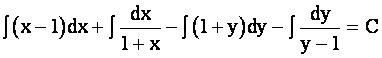 .
.
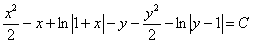
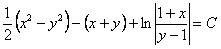
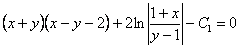 , где
, где 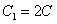 . Получили общий интеграл.
. Получили общий интеграл.
ПРИМЕР 11.2.3. Проинтегрировать уравнение 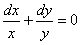 .
.
Решение.
Данное уравнение — есть уравнение с разделенными переменными. Проинтегрируем данное уравнение 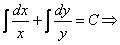
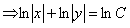 (так как левая часть выражается через натуральный логарифм, то постоянную
(так как левая часть выражается через натуральный логарифм, то постоянную 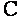 удобнее в данном случае записать как
удобнее в данном случае записать как 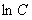 ).
).
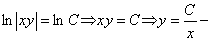 общее решение, с геометрической точки зрения определяет семейство гипербол.
общее решение, с геометрической точки зрения определяет семейство гипербол.
ПРИМЕР 11.2.4. Найти кривую, обладающую тем свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.
Решение.
Пусть 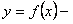 уравнение искомой кривой,
уравнение искомой кривой, 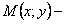 произвольная точка кривой.
произвольная точка кривой.
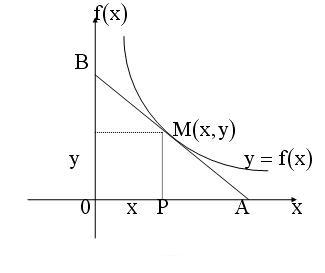
рис 11.2.1
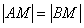 , т.е.
, т.е.
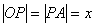 . Из
. Из 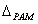
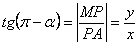 , так как
, так как 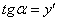 , то
, то 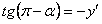 , тогда
, тогда 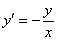 . Получили дифференциальное уравнение с разделяющими переменными, интегрируя его, получим
. Получили дифференциальное уравнение с разделяющими переменными, интегрируя его, получим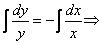
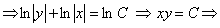
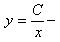 семейство интегральных кривых, удовлетворяющих условию задачи.
семейство интегральных кривых, удовлетворяющих условию задачи.
ПРИМЕР 11.2.5. Материальная точка с массой 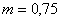 г погружается в жидкость без начальной скорости. Сила сопротивления жидкости пропорциональна скорости погружения
г погружается в жидкость без начальной скорости. Сила сопротивления жидкости пропорциональна скорости погружения 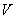 . Коэффициент пропорциональности
. Коэффициент пропорциональности 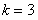 . Найти зависимость погружения от времени.
. Найти зависимость погружения от времени.
Решение.
В момент времени 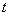 точка находится под действием силы тяжести
точка находится под действием силы тяжести 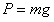 и силы сопротивления жидкости
и силы сопротивления жидкости 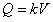 . Сила P направлена в сторону движения, а
. Сила P направлена в сторону движения, а 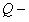 в сторону противоположную движению, поэтому их равнодействующая
в сторону противоположную движению, поэтому их равнодействующая 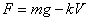 .
.
Так как материальная точка погружается в жидкость под действием силы 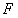 , то по второму закону Ньютона эта же сила равна
, то по второму закону Ньютона эта же сила равна 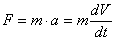 . Приравнивая оба выражения для
. Приравнивая оба выражения для 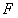 , получим
, получим 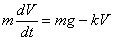 , но по условию
, но по условию 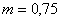 г, а
г, а 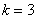 .
. 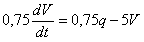 сократим на
сократим на 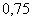 ,
, 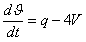 .
.
Получили уравнение с разделяющими переменными. Разделив переменные и проинтегрировав, получим
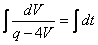 .
. 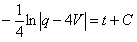 .
.

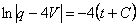 ;
; 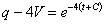 ;
; 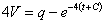 ;
;
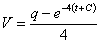 или
или 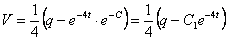 , где
, где 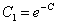 .
.
Для нахождения 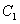 воспользуемся начальным условием
воспользуемся начальным условием 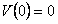 .
.
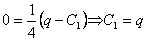 .Тогда частное решение будет иметь вид
.Тогда частное решение будет иметь вид
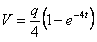 .
.
Задачи и примеры для самостоятельного решения
Решите уравнения:
11.2.5 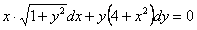 |
Отв. 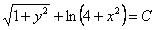 |
11.2.6 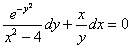 |
Отв. 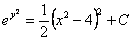 |
11.2.7 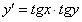 |
Отв. 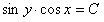 |
11.2.8 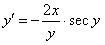 |
Отв. 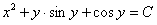 |
11.2.9 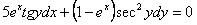 |
Отв. 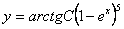 |
| Найти частные решения уравнений | |
11.2.10 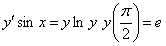 |
Отв. 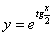 |
11.2.11 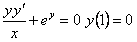 |
Отв. 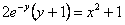 |
11.2.12 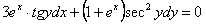 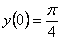 |
Отв. 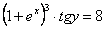 |
11.2.13 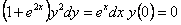 |
Отв. 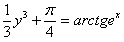 |
 11.2.14 Кривая проходит через точку
11.2.14 Кривая проходит через точку 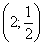 . В произвольной точке этой кривой проведена касательная. Точка пересечения касательной с осью
. В произвольной точке этой кривой проведена касательная. Точка пересечения касательной с осью 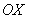 имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.
имеет абсциссу вдвое большую, чем абсцисса точки касания. Найти кривую.
Ответ: 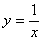
11.2.15 Составить уравнение кривой, проходящей через точку 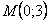 , если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания.
, если угловой коэффициент касательной в любой точке кривой равен произведению координат точки касания.
Ответ: 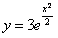 .
.
11.2.16 Найти время, в течение которого вся вода вытекает из конической воронки, если известно, что половина воды вытекает в 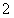 мин.
мин.
Ответ: 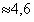 мин.
мин.
11.2.17 В комнате, где температура 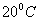 , некоторое тело остыло за
, некоторое тело остыло за 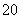 мин от
мин от 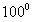 до
до 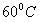 . Найти закон охлаждения тела; через сколько минут оно остынет до
. Найти закон охлаждения тела; через сколько минут оно остынет до 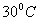 ? Повышением температуры в комнате пренебречь.
? Повышением температуры в комнате пренебречь.
Ответ: 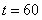 мин.
мин.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >