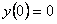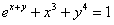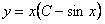ОПРЕДЕЛЕНИЕ 11.2.16 Уравнение вида 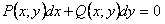 называется уравнением в полных дифференциалах, если выражение
называется уравнением в полных дифференциалах, если выражение
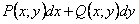 (11.2.4)
(11.2.4)
представляет собой полный дифференциал некоторой функции u(x;y), т.е.,
если  .
.
Согласно определения уравнение (11.2.4) примет вид 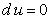 . Отсюда
. Отсюда 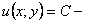 общий интеграл данного уравнения.
общий интеграл данного уравнения.
Не всякое уравнение (11.2.4) будет уравнением в полных дифференциалах. Для того, чтобы уравнение (11.2.4) было уравнением в полных дифференциалах достаточно выполнения условия
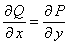 . (11.2.5)
. (11.2.5)
Если уравнение (11.2.4) – уравнение в полных дифференциалах, то
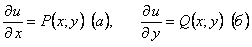 . Решая уравнение (а) получим, что
. Решая уравнение (а) получим, что 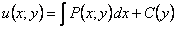 , требуется найти
, требуется найти 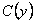 , которое находим, решая уравнение (б).
, которое находим, решая уравнение (б).  . Из последнего уравнения находим
. Из последнего уравнения находим 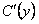 , а следовательно и
, а следовательно и 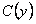 .
.
Функция 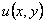 может быть найдена по формуле
может быть найдена по формуле
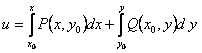 ,(11.2.6)
,(11.2.6)
где x0 и y0 произвольны; их выбор ограничен единственным условием – интеграл в правой части должна иметь смысл.
Замечание 1. Если дифференциальное уравнение первого порядка является одновременно однородным и в полных дифференциалах, то общий интеграл находится по формуле
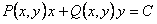 . (11.2.7)
. (11.2.7)
Если в уравнении (11.2.4) условие (11.2.5) не выполняется, т.е. 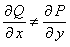 , то уравнение (11.2.4) не является уравнением в полных дифференциалах. Иногда удается подобрать такой множитель
, то уравнение (11.2.4) не является уравнением в полных дифференциалах. Иногда удается подобрать такой множитель 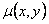 , который называется интегрирующим множителем, при умножении которого на уравнение получается уравнение в полных дифференциалах.
, который называется интегрирующим множителем, при умножении которого на уравнение получается уравнение в полных дифференциалах.
Если у данного уравнения существует интегрирующий множитель, зависящий только от x, то он находится по формуле
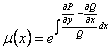 , (11.2.8)
, (11.2.8)
зависящий только от 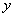 по формуле
по формуле
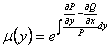 . (11.2.9)
. (11.2.9)
ПРИМЕР 11.2.57 Решить уравнение
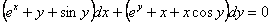 .
.
Решение.
Проверим, является ли данное уравнение в полных дифференциалах. 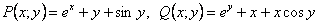 .
.
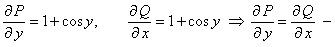 уравнение в полных дифференциалах.
уравнение в полных дифференциалах.
Следовательно, левая часть уравнения есть полный дифференциал некоторой функции 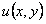 , т.е.
, т.е.
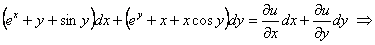
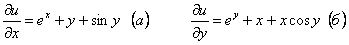 .
.
Проинтегрируем уравнение (а) по 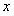 :
: 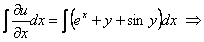
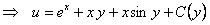 .
.
От найденного u берем частную производную по y и приравниваем Q(x,y)
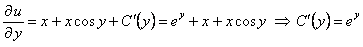 интегрируя,
интегрируя, 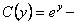 подставляем в
подставляем в 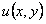
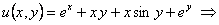
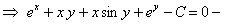 общий интеграл.
общий интеграл.
ПРИМЕР 11.2.58 Решить уравнение по формуле (11.2.6)
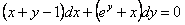 .
.
Решение.
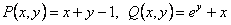 .
.
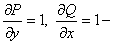 уравнение в полных дифференциалах.
уравнение в полных дифференциалах.
Найдем общий интеграл по формуле (11.2.6) 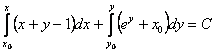 .
.
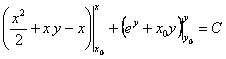 ;
;
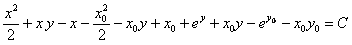 .
.
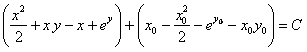 .
.
Пусть 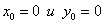 , тогда
, тогда 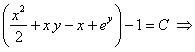
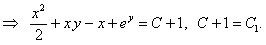
 общий интеграл.
общий интеграл.
ПРИМЕР 11.2.59 Решить уравнение 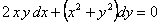 .
.
Решение.
Данное уравнение однородное, так как функции 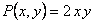 и
и 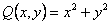 однородные функции второй степени. Одновременно данное уравнение является уравнением в полных дифференциалах, так как
однородные функции второй степени. Одновременно данное уравнение является уравнением в полных дифференциалах, так как 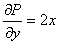 и
и 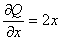 . Согласно замечания (11.2.4), общий интеграл будет иметь вид
. Согласно замечания (11.2.4), общий интеграл будет иметь вид
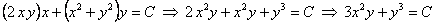 .
.
ПРИМЕР 11.2.60 Решить уравнение
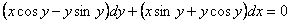 .
.
Решение.
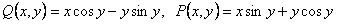
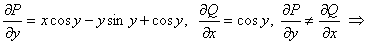 уравнение не в полных дифференциалах.
уравнение не в полных дифференциалах.
Исследуем выражение 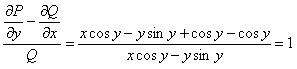 . Данное уравнение имеет интегрирующий множитель, зависящий только от
. Данное уравнение имеет интегрирующий множитель, зависящий только от 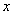 . Найдем этот интегрирующий множитель.
. Найдем этот интегрирующий множитель.
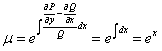 . Умножив исходное уравнение на
. Умножив исходное уравнение на 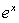 , получим:
, получим: 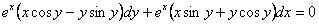 .
.
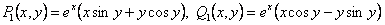 .
.
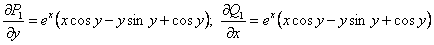
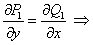 полученное уравнение в полых дифференциалах. Таким образом, имеем
полученное уравнение в полых дифференциалах. Таким образом, имеем
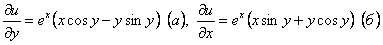 . Интегрируя уравнение (а) по y, получим:
. Интегрируя уравнение (а) по y, получим:
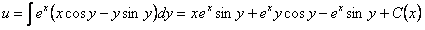
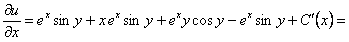
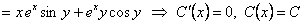 .
.
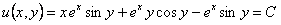 .
.
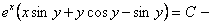 общий интеграл.
общий интеграл.
Примеры и задачи для самостоятельного решения
Найти общий интеграл.
11.2.61 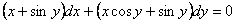 ; ;Отв. 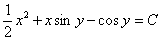 |
11.2.62 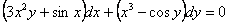 ; ;Отв. 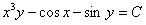 |
11.2.63 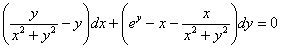 Отв. 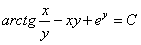 |
11.2.64 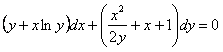 ; ;Отв. 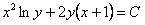 |
| Найти частный интеграл. |
11.2.65 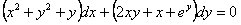 , ,
начальное условие: |
11.2.66 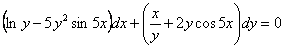 , ,начальное условие: 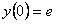 Отв. 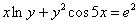 |
11.2.67 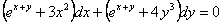
начальное условие: |
11.2.68 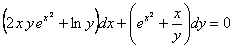 , ,начальное условие: 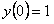 Отв. 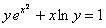 |
11.2.69 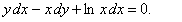 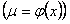 Отв. 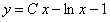 |
11.2.70 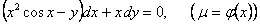
Отв. |
11.2.71 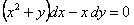 Отв. 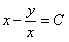 |
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
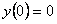 .
.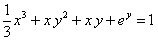 .
.