ОПРЕДЕЛЕНИЕ 11.2.24 Системой называется совокупность дифференциальных уравнений, содержащих функции 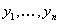 и их производные. Максимальный порядок производной называется порядком системы.
и их производные. Максимальный порядок производной называется порядком системы.
ОПРЕДЕЛЕНИЕ 11.2.25 Система дифференциальных уравнений, разрешенных относительно старших производных, называется нормальной. Например, нормальная система первого порядка имеет вид:
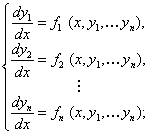 (11.2.26)
(11.2.26)
ОПРЕДЕЛЕНИЕ 11.2.26 Решением называется набор функций 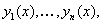
 которые после подстановки в систему обращают каждое ее уравнение в верное равенство.
которые после подстановки в систему обращают каждое ее уравнение в верное равенство.
Задача Коши для системы (11.2.26) заключается в нахождении такого решения, которое удовлетворяет начальным данным в виде
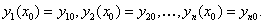 (11.2.27)
(11.2.27)
ОПРЕДЕЛЕНИЕ 11.2.27 Общим решением системы (11.2.26) называется набор функций 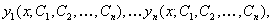 которые
которые
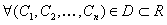 являются решением (11.2.26); кроме того, для любых начальных данных вида (14.2) принадлежащих области определения системы, существует
являются решением (11.2.26); кроме того, для любых начальных данных вида (14.2) принадлежащих области определения системы, существует 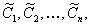 при которых функции
при которых функции 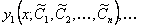 ,
,
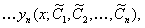 удовлетворяют начальным данным (11.2.27). Решение, соответствующее какому-либо конкретному набору констант, называется частным решением.
удовлетворяют начальным данным (11.2.27). Решение, соответствующее какому-либо конкретному набору констант, называется частным решением.
Разберем решение систем на примере линейных систем, то есть таких в которых функции из правых частей линейны по своим аргументам
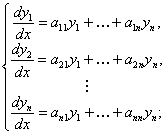 (11.2.28)
(11.2.28)
коэффициенты 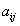 -известные константы.
-известные константы.
Один из методов заключается в сведении системы к дифференциальному уравнению на одну из неизвестных функций. Продифференцируем, например, первое уравнение
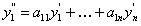 .
.
В полученное уравнение вместо 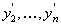
 подставляем выражения для них взятых из системы. Получаем уравнение, которое запишем в виде:
подставляем выражения для них взятых из системы. Получаем уравнение, которое запишем в виде:
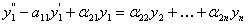 (11.2.29)
(11.2.29)
Коэффициенты αij легко пересчитываются через коэффициенты исходной системы. Проделывая эту процедуру далее, имеем
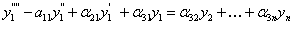 (11.2.30)
(11.2.30)

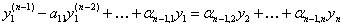 (11.2.31)
(11.2.31)
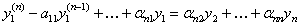 (11.2.32)
(11.2.32)
Рассматривая первое уравнение системы (11.2.28) и уравнения (11.2.29)-( 11.2.32) как линейную алгебраическую систему на функции 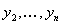 можно получить для них выражения через функцию
можно получить для них выражения через функцию 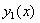 и ее производные
и ее производные 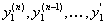 . Подставляя эти выражения в последнее уравнение (11.2.32), получаем линейное дифференциальное уравнение n-го порядка на функцию
. Подставляя эти выражения в последнее уравнение (11.2.32), получаем линейное дифференциальное уравнение n-го порядка на функцию 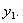 Решая полученное уравнение тем или иным способом находим
Решая полученное уравнение тем или иным способом находим 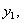 затем по полученным формулам находим
затем по полученным формулам находим 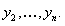
ПРИМЕР 11.2.130 Найти общее решение системы дифференциальных уравнений 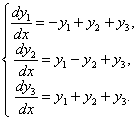
Решение.
Продифференцируем первое уравнение
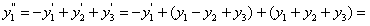
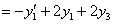 . Или
. Или
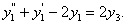 (11.2.33)
(11.2.33)
Дифференцируем далее и получаем
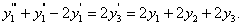
Или
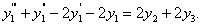
Чтобы получить уравнение для 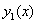 , необходимо выразить
, необходимо выразить 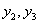 через
через 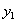 и ее производные. Рассмотрим первое уравнение исходной системы и уравнение (11.2.33), записанные в виде
и ее производные. Рассмотрим первое уравнение исходной системы и уравнение (11.2.33), записанные в виде
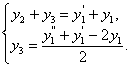
Эта линейная алгебраическая система для 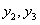 решается тривиально
решается тривиально
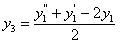 ,
,
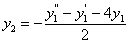 . (11.2.34)
. (11.2.34)
Подставляем эти выражения в правую часть (11.2.33)
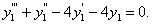 (11.2.35)
(11.2.35)
Уравнение (14.10) имеет характеристическое уравнение вида 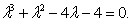 Один из корней
Один из корней 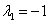 легко угадывается. Два других находятся как корни уравнения
легко угадывается. Два других находятся как корни уравнения 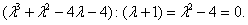 Они равны
Они равны 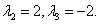
Следовательно, общее решение уравнения (11.2.35) имеет вид
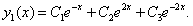
Из (11.2.35) находим 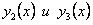
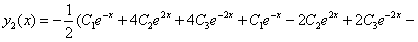
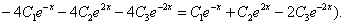
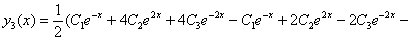
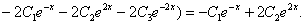
Рассмотрим метод решения систем дифференциальных уравнений с помощью матриц на примере систем второго порядка
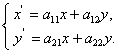 (11.2.36)
(11.2.36)
Будем искать решение в виде 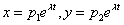 . Определим при каких
. Определим при каких 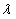 такое решение существует. Подставим выражения для
такое решение существует. Подставим выражения для 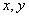 в систему, и после сокращения на
в систему, и после сокращения на 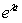 , получаем
, получаем
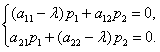 (11.2.37)
(11.2.37)
Эта линейная алгебраическая система имеет ненулевые решения только тогда, когда определитель соответствующей матрицы равен 0:
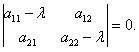 (11.2.38)
(11.2.38)
Уравнение (11.2.38) называется характеристическим уравнением системы (11.2.36), его решения – характеристическими числами. Это уравнение имеет два корня 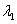 и
и 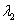 (вообще говоря, комплексные). Рассмотрим три различных случая.
(вообще говоря, комплексные). Рассмотрим три различных случая.
1) 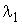 ,
, 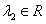 ,
, 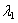
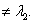
В этом случае система имеет два частных решения, соответствующие различным собственным числам: первое-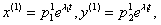 второе —
второе —
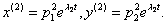 В качестве
В качестве 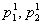 и
и 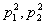 берутся какие-либо решения системы (11.2.37) с соответствующими
берутся какие-либо решения системы (11.2.37) с соответствующими 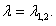 Общее решение системы выписывается как линейная комбинация частных решений с произвольными коэффициентами:
Общее решение системы выписывается как линейная комбинация частных решений с произвольными коэффициентами:
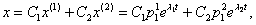
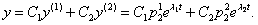
2)
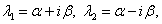
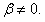
Пусть 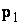 и
и 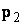 — решения системы (11.2.37), соответствующее
— решения системы (11.2.37), соответствующее 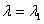 .Частным решением является пара комплексных функций
.Частным решением является пара комплексных функций 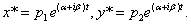 Частными вещественными решениями являются следующие пары функции, определенные как вещественная и мнимая части
Частными вещественными решениями являются следующие пары функции, определенные как вещественная и мнимая части 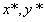 :
:
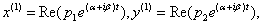
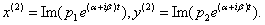
Их линейная комбинация и даст выражения для общего решения
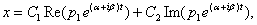
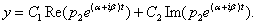
3) 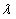 — вещественный корень кратности 2.
— вещественный корень кратности 2.
Общее решение в этом случае имеет вид
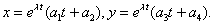 (11.2.39)
(11.2.39)
Здесь 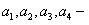 неизвестные константы, но только две из них могут быть произвольными. Чтобы определить их, подставим выражения (11.2.39) в систему 11.2.39. Отдельно приравнивая свободные члены и члены с множителями
неизвестные константы, но только две из них могут быть произвольными. Чтобы определить их, подставим выражения (11.2.39) в систему 11.2.39. Отдельно приравнивая свободные члены и члены с множителями 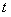 , получим два различных уравнения. Полагая, например,
, получим два различных уравнения. Полагая, например, 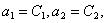 находим
находим 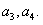
ПРИМЕР 11.2.131 Найти общее решение системы уравнений.
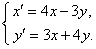
Решение.
Разыскиваем решение в виде 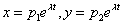 . На
. На 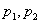 и
и 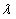 получаем систему
получаем систему
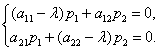
Эта алгебраическая система имеет ненулевые решения только при 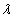 равном корню характеристического многочлена
равном корню характеристического многочлена
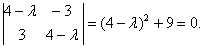
Корни 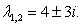 Найдем
Найдем 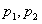 ,соответствующие значения
,соответствующие значения 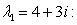
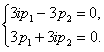
Система имеет бесконечно много решений (ее строки пропорциональны, определитель равен 0). Положим 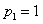 , тогда
, тогда 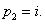 Пару частных решений выпишем как вещественную и мнимую часть функций
Пару частных решений выпишем как вещественную и мнимую часть функций 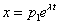 и
и 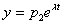 :
:
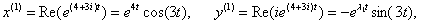

Общее решение
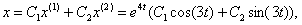
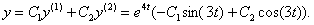
Примеры для самостоятельного решения
11.2.132 Найти общее решение системы уравнений: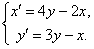 Отв.
Отв. 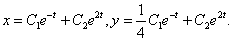
11.2.133 Найти решение задачи Коши: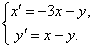
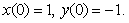
Отв. 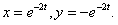
Найти общее решение системы уравнений
11.2.134 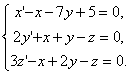
Отв.
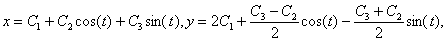
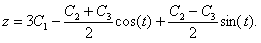
11.2.135 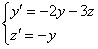 .
.
Отв. 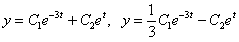 .
.
11.2.136. 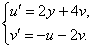
Отв. 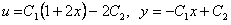 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >