ТЕОРЕМА 12.1.5 Если числовой ряд 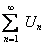 сходится, то его общий член при неограниченном возрастании n стремится к нулю, то есть
сходится, то его общий член при неограниченном возрастании n стремится к нулю, то есть 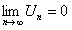 .
.
Доказательство. Дан сходящийся числовой ряд 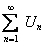 , а это значит, что
, а это значит, что
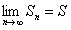 ,(12.1.7)
,(12.1.7)
но и
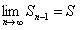 , так как
, так как 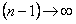 при
при 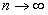 (12.1.8)
(12.1.8)
Вычитая из (12.1.7) (12.1.8), получим
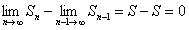 или
или
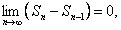 но
но 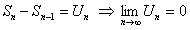 .
.
Замечание. Если для некоторого ряда 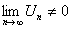 , то такой ряд расходится (достаточный признак расходимости).
, то такой ряд расходится (достаточный признак расходимости).
ПРИМЕР 12.1.2 Гармонический ряд. Ряд вида
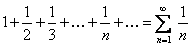 называется гармоническим. Для этого ряда выполняется необходимое условие сходимости
называется гармоническим. Для этого ряда выполняется необходимое условие сходимости 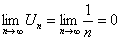 .
.
Покажем, что этот ряд расходится. Известно, что возрастающая последовательность 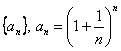 сходится и ее предел равен e:
сходится и ее предел равен e:
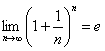 ; при этом
; при этом 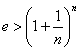 . Логарифмируя это неравенство, имеем
. Логарифмируя это неравенство, имеем  или, деля обе части на
или, деля обе части на 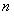 ,
, 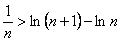 .
.
При 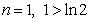 ;
;
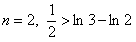 ;
;
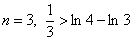 ;
;
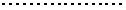
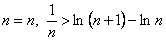 .
.
Частичная сумма 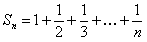 гармонического ряда, каждый член которой больше соответствующего члена суммы вида
гармонического ряда, каждый член которой больше соответствующего члена суммы вида
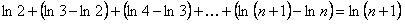 , удовлетворяет неравенству
, удовлетворяет неравенству 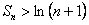 , но
, но 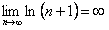 , откуда следует, что
, откуда следует, что 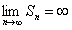 .
.
Из рассмотренного примера следует, что рассмотренный признак не является достаточным признаком сходимости ряда.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >