ТЕОРЕМА 12.1.6 Если ряд 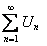 сходится и
сходится и 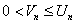
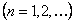 , то и ряд
, то и ряд 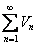 сходится. Если же ряд
сходится. Если же ряд 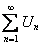 расходится, а
расходится, а 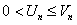 , то ряд
, то ряд 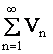 расходится.
расходится.
Доказательство. Пусть 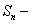 частичная сумма ряда
частичная сумма ряда 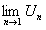 ,
,  частичная сумма ряда
частичная сумма ряда 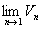 . Так как ряд
. Так как ряд 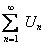 сходится, то его частичная сумма ограничена, то есть при всех
сходится, то его частичная сумма ограничена, то есть при всех 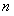
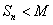 , где
, где 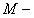 некоторое число. Так как
некоторое число. Так как 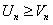 , то
, то 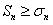 , а это значит, что частичная сумма
, а это значит, что частичная сумма 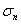 ряда
ряда 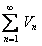 также ограничена, а этого достаточно для сходимости ряда
также ограничена, а этого достаточно для сходимости ряда 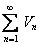 с неотрицательными членами.
с неотрицательными членами.
Если же ряд 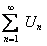 расходится, то ряд
расходится, то ряд 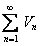 также расходится, так как предположив, что ряд
также расходится, так как предположив, что ряд 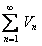 сходится и
сходится и 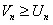 , по условию, по выше доказанному должен сходиться и ряд
, по условию, по выше доказанному должен сходиться и ряд 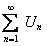 , что противоречит условию. Значит, ряд
, что противоречит условию. Значит, ряд 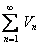 расходится.
расходится.
ПРИМЕР 12.1.3 Пользуясь теоремой 12.6, исследовать сходимость ряда 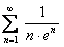 .
.
Решение. Проверим, выполняется ли для данного ряда необходимый признак сходимости знакоположительных рядов 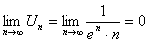 , ряд может сходиться.
, ряд может сходиться.
Для доказательства сходимости применим теорему 12.1.6. Для сравнения рассмотрим ряд 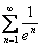 , который сходится, так как
, который сходится, так как 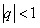 , причем
, причем 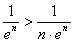 . Следовательно, сходится и ряд
. Следовательно, сходится и ряд 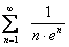 .
.
Следствие. Если существует конечный и отличный от нуля предел 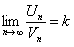 , то из сходимости ряда с общим членом
, то из сходимости ряда с общим членом 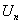 следует сходимость ряда с общим членом
следует сходимость ряда с общим членом 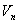 , и из расходимости первого ряда следует расходимость второго.
, и из расходимости первого ряда следует расходимость второго.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >