Интегральный признак Коши: Пусть члены ряда

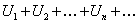 (12.1.17)

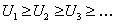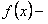положительны и не возрастают, то есть и непрерывная невозрастающая функция, причем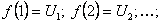 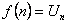, тогда:

1) если несобственный интеграл 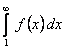сходится, то сходится и ряд (12.1.17);

2) если интеграл 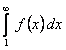расходится, то расходится и ряд (12.1.17).

Доказательство. Для доказательства изобразим члены ряда (12.1.17) геометрически, откладывая по оси 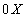номера 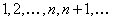членов ряда, а по оси ординат – соответствующие значения членов ряда 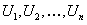, (рис.12.1).

На этом же чертеже построим график непрерывной невозрастающей функции 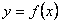, удовлетворяющей условиям теоремы. Сравнивая площади ступенчатых фигур, криволинейной трапеции, из геометрического смысла определенного интеграла имеем

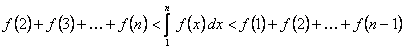или с учетом, что 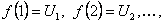получим

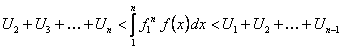.(12.1.18)

Так как частичная сумма 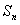ряда (12.17) равна ,

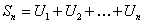то левая часть (12.1.18) есть 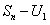, а правая 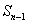, тогда

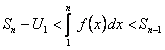.(12.1.19)

1. Предположим, что интеграл 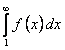сходится. Так как

,

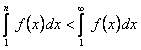то в силу неравенства (12.19) будем иметь

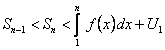,(12.1.20)

то есть частичные суммы ограничены при всех значениях 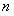, а это значит по признаку сравнения (12.1.17) сходится.

2. Предположим, что интеграл 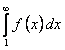расходится, то есть

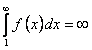. Из расходимости интеграла 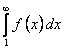следует, что интеграл

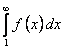неограниченно возрастает при 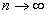. Тогда в силу правой части

неравенства (12.1.19) 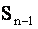также неограниченно возрастает при 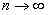, то есть ряд расходится.

ПРИМЕР 12.1.6 Исследовать сходимость ряда , .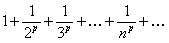

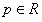Решение. Рассмотрим случай, когда 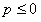. Тогда 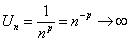, так как .

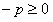Для данного случая необходимое условие сходимости не выполняется, ряд расходится. Применим интегральный признак для случая 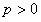, положим 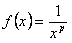. Это функция при 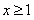непрерывная и монотонно убывающая. Рассмотрим интеграл

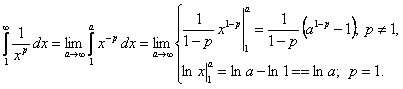
2. 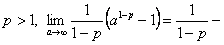предел конечен, интеграл сходится, следовательно, ряд сходится.

3. 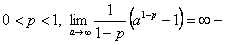интеграл расходится, тогда расходится ряд.

4. 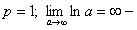интеграл расходится, тогда расходится ряд.

Итак, ряд 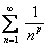сходится 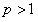при , при 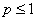расходится. Данный ряд называется обобщенным гармоническим рядом. При 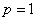получаем гармонический ряд 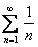, который расходится.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >