Рассмотрим ряд, члены которого имеют чередующиеся знаки, то есть ряд вида
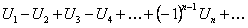 , где
, где
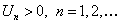 или
или 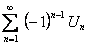 . (12.1.23)
. (12.1.23)
ТЕОРЕМА Лейбница. Если у знакочередующегося ряда 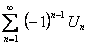 ,
,
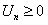 , абсолютные величины членов ряда убывают
, абсолютные величины членов ряда убывают 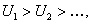 и
и 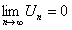 , то ряд сходится, его сумма положительна и не превосходит первого члена.
, то ряд сходится, его сумма положительна и не превосходит первого члена.
Доказательство. 1. Рассмотрим сумму 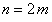 первых членов ряда
первых членов ряда 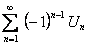 , то есть
, то есть
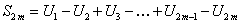 .(12.1.24)
.(12.1.24)
Правую часть (12.1.24) запишем в виде
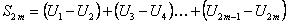 .(12.1.25)
.(12.1.25)
Из условия теоремы 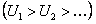 следует, что разность в скобках (12.1.25) положительна. Следовательно, сумма
следует, что разность в скобках (12.1.25) положительна. Следовательно, сумма 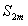 положительна
положительна 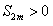 и возрастает с возрастанием
и возрастает с возрастанием 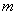 .
.
Докажем, что она ограничена. Для этого представим 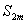 следующим образом:
следующим образом:
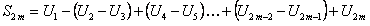 .(12.1.26)
.(12.1.26)
В силу условия 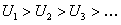 каждая разность в скобках (12.1.26) положительна. Поэтому в результате вычитания выражения в скобках из
каждая разность в скобках (12.1.26) положительна. Поэтому в результате вычитания выражения в скобках из 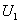 получим число, меньшее, чем
получим число, меньшее, чем 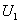 , то есть
, то есть 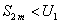 .
.
Таким образом, 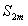 при возрастании m возрастает и ограничена сверху. Следовательно, по теореме о пределе монотонной переменной она имеет предел
при возрастании m возрастает и ограничена сверху. Следовательно, по теореме о пределе монотонной переменной она имеет предел 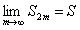 , причем
, причем 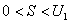 .
.
2. Чтобы доказать сходимость ряда 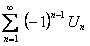 , нужно доказать еще, что «нечетные» частичные суммы также стремятся к
, нужно доказать еще, что «нечетные» частичные суммы также стремятся к 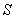 . Рассмотрим сумму
. Рассмотрим сумму 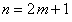 первых членов ряда
первых членов ряда 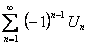
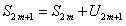 . (12.1.27)
. (12.1.27)
По условию теоремы 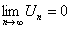 , следовательно,
, следовательно, 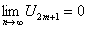 ,
,
тогда
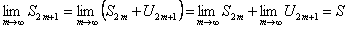 .
.
Тем самым доказали, что 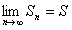 (как при
(как при 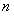 четном, так и при нечетном). Следовательно, ряд
четном, так и при нечетном). Следовательно, ряд 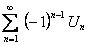 сходится.
сходится.
Замечание 1. На рис. 12.2 наглядно показано, что по мере возрастания числа членов частичные суммы 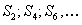 возрастают, а частичные суммы
возрастают, а частичные суммы 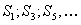 убывают, приближаясь к сумме ряда
убывают, приближаясь к сумме ряда 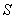 .
.
ПРИМЕР 12.1.8 Исследовать сходимость ряда
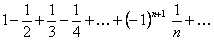 .
.
Решение. Данный ряд знакопеременный. Для исследования его сходимости составляем ряд из абсолютных величин его членов, то есть ряд вида
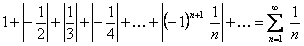 .
.
Полученный ряд гармонический, который расходится. Применим теорему Лейбница, так как ряд знакочередующийся. Проверим выполнение условий этой теоремы: 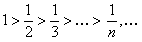 , то есть первое условие выполняется.
, то есть первое условие выполняется. 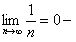 второе условие также выполнено. Следовательно, ряд сходится, но ряд, составленный из абсолютных величин его членов расходится, то согласно определению 8 этот ряд сходится условно.
второе условие также выполнено. Следовательно, ряд сходится, но ряд, составленный из абсолютных величин его членов расходится, то согласно определению 8 этот ряд сходится условно.
Замечание 2. Теорема Лейбница позволяет оценить ошибку, которая получается, если заменить его сумму 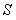 частичной суммой
частичной суммой 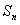 . При такой замене мы отбрасываем все члены ряда, начиная с
. При такой замене мы отбрасываем все члены ряда, начиная с 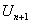 , то есть получаем ряд вида
, то есть получаем ряд вида
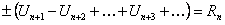 .(12.1.28)
.(12.1.28)
Здесь 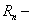 остаток ряда, представляет собой знакочередующийся ряд, удовлетворяющий теореме Лейбница. По теореме Лейбница сумма ряда (12.1.28) не превосходит по абсолютной величине члены
остаток ряда, представляет собой знакочередующийся ряд, удовлетворяющий теореме Лейбница. По теореме Лейбница сумма ряда (12.1.28) не превосходит по абсолютной величине члены 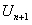 , то есть
, то есть 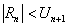 . Таким образом, пользуясь приближенным равенством
. Таким образом, пользуясь приближенным равенством 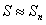 , допускают ошибку, которая меньше абсолютной величины первого из отбрасываемых членов.
, допускают ошибку, которая меньше абсолютной величины первого из отбрасываемых членов.
ПРИМЕР 12.1.9 Вычислить сумму ряда
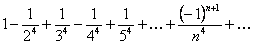 с точностью
с точностью 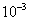 .
.
Решение. Исследуем на сходимость данный ряд. Для этого составим ряд из абсолютных величин его членов, то есть ряд вида
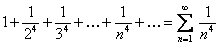 . Полученный ряд гармонический с
. Полученный ряд гармонический с 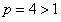 . Поэтому он сходится. Тогда по признаку сравнения сходится и ряд
. Поэтому он сходится. Тогда по признаку сравнения сходится и ряд
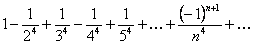 . Но этот ряд знакочередующийся. Согласно замечанию 2 ошибка, которая получается при замене данного ряда его частичной суммой, не превосходит по абсолютной величине члена
. Но этот ряд знакочередующийся. Согласно замечанию 2 ошибка, которая получается при замене данного ряда его частичной суммой, не превосходит по абсолютной величине члена 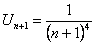 . Чтобы достичь заданной точности, достаточно положить
. Чтобы достичь заданной точности, достаточно положить  , откуда находим наименьшее
, откуда находим наименьшее 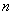 , удовлетворяющее этому неравенству, то есть
, удовлетворяющее этому неравенству, то есть 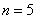 . Для вычисления суммы ряда с точностью
. Для вычисления суммы ряда с точностью 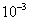 достаточно взять сумму первых пяти слагаемых, то есть
достаточно взять сумму первых пяти слагаемых, то есть
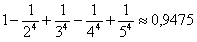 . Сумма данного ряда с точностью
. Сумма данного ряда с точностью 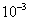 равна
равна 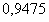 .
.
Замечание 3. Теорема Лейбница остается в силе, если члены знакочередующегося ряда начинают убывать, начиная с некоторого 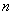 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >