Дан степенной ряд 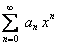 . Требуется определить его интервал сходимости. Для решения поставленной задачи поступаем следующим образом:
. Требуется определить его интервал сходимости. Для решения поставленной задачи поступаем следующим образом:
а) определяем радиус сходимости степенного ряда по формулам (12.1.43) или (12.1.44);
б) записываем интервал сходимости 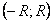 ;
;
в) проверим поведение ряда на концах интервала 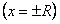 . В ряд вместо
. В ряд вместо 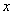 подставляем
подставляем 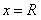 или
или 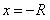 , в результате чего получаем знакоположительные или знакочередующиеся числовые ряды, к которым применяем соответствующие признаки сходимости;
, в результате чего получаем знакоположительные или знакочередующиеся числовые ряды, к которым применяем соответствующие признаки сходимости;
г) если при 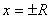 числовые ряды сходятся, то данный степенной ряд сходится на отрезке
числовые ряды сходятся, то данный степенной ряд сходится на отрезке 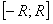 .
.
Если при 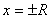 числовые ряды расходятся, то данный степенной ряд сходится на интервале
числовые ряды расходятся, то данный степенной ряд сходится на интервале 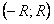 .
.
Если при 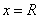 числовой ряд сходится, а при
числовой ряд сходится, а при 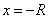 расходится или, наоборот, при
расходится или, наоборот, при 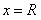 расходится, а при
расходится, а при 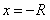 сходится, то данный степенной ряд сходится на полуинтервале
сходится, то данный степенной ряд сходится на полуинтервале 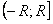 или
или 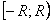 .
.
ПРИМЕР 12.1.15 Определить интервал сходимости ряда
 .
.
Решение. Определим радиус сходимости по формуле (12.1.43), для чего запишем 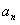 и
и 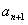 .
.
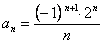 и
и 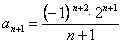 , тогда
, тогда
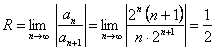 .
.
Так как 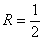 , то интервал сходимости будет иметь вид
, то интервал сходимости будет иметь вид 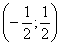 .
.
Проверим поведение ряда на концах интервала. Подставим в данный ряд вместо 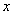 число:
число: 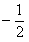 , получим числовой ряд
, получим числовой ряд 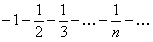 . Полученный числовой знакопостоянный ряд является гармоническим рядом и расходится. При
. Полученный числовой знакопостоянный ряд является гармоническим рядом и расходится. При 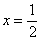 получаем числовой знакочередующийся ряд
получаем числовой знакочередующийся ряд 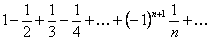 , который сходится, так как для него выполняются условия теоремы Лейбница, а именно: члены ряда убывают по абсолютной величине, то есть
, который сходится, так как для него выполняются условия теоремы Лейбница, а именно: члены ряда убывают по абсолютной величине, то есть 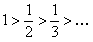 и
и 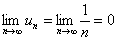 . Следовательно, данный степенной ряд сходится на полуинтервале
. Следовательно, данный степенной ряд сходится на полуинтервале 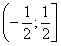 .
.
Отметим, что если 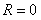 , то интервал сходимости вырождается в точку, если
, то интервал сходимости вырождается в точку, если 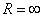 , то интервал сходимости
, то интервал сходимости 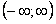 .
.
ПРИМЕР 12.1.16 Определить интервал сходимости ряда
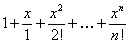 .
.
Решение. Вычислим радиус сходимости
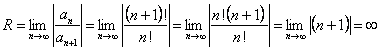 .
.
Таким образом, интервал сходимости этого ряда состоит из всех вещественных чисел 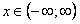 .
.
ПРИМЕР 12.1.17 Определить интервал сходимости ряда
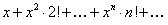 .
.
Решение. Вычислим радиус сходимости
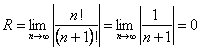 . Итак,
. Итак, 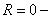 интервал сходимости вырождается в точку, то есть данный ряд сходится лишь при
интервал сходимости вырождается в точку, то есть данный ряд сходится лишь при 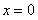 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >