ТЕОРЕМА 12.14 Степенной ряд сходится на любом отрезке, лежащем внутри интервала сходимости.
Доказательство. Пусть отрезок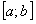 
лежит внутри интервала сходимости 
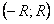ряда 
.
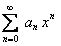Тогда найдется такое число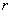 
, 
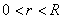, что отрезок 
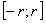будет содержать отрезок 
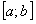. Ряд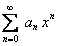 
абсолютно сходится при 
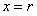, то есть сходится ряд 
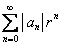. Но для всех 
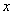отрезка 
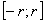выполняется неравенство 
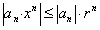, которое означает, что ряд 
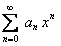на отрезке 
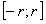по признаку Вейерштрасса равномерно сходится на этом отрезке, в частности, он равномерно сходится и на отрезке 
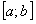, что и требовалось доказать. Из доказанной теоремы вытекает следующее следствие.
Следствие. Сумма степенного ряда является непрерывной функцией на интервале сходимости.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
