Рассмотрим разложение в ряд Маклорена функции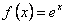

Так как .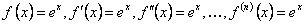

Для любого фиксированного 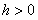при всех 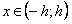и всех n=0,1,2,… 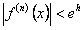или .

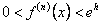Таким образом, условие теоремы (1) для 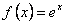выполнено, поэтому функция 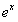раскладывается в ряд Тейлора на любом конечном интервале, а значит, и на всей действительной оси. Если 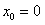, то 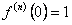; получим разложение функции в ряд Маклорена, который имеет вид

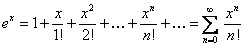    .          (12.1.56)

Полученный ряд можно использовать для разложения в ряд Маклорена сложных показательных функций.

ПРИМЕР 12.1.19 Разложить функцию 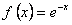в ряд Маклорена. Для решения поставленной задачи воспользуемся выражением (12.1.56), заменив 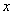на :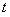

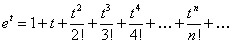.              (12.1.57)

Подставим 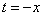 ; получим искомый ряд

.

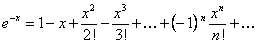который сходится абсолютно при любых .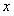

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >