Пусть 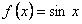 . Тогда
. Тогда
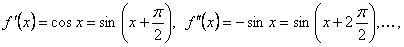
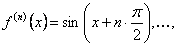
поэтому 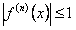 для всех действительных
для всех действительных 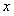 . Согласно теореме (12.14) функция
. Согласно теореме (12.14) функция 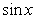 раскладывается в степенной ряд по всей действительной оси.
раскладывается в степенной ряд по всей действительной оси.
Полагая 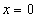 , найдем
, найдем 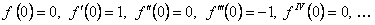 .
.
Следовательно,
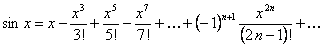
или
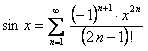 . (12.1.58)
. (12.1.58)
Ряд (12.1.58) есть разложение 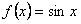 в ряд Маклорена.
в ряд Маклорена.
Разложение 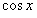 в ряд Маклорена можно получить, повторяя предыдущие рассуждения; так как ряд (12.1.56) сходится на всей действительной оси, то на основании теоремы (12.1.15) его можно почленно дифференцировать, в результате чего получим разложение
в ряд Маклорена можно получить, повторяя предыдущие рассуждения; так как ряд (12.1.56) сходится на всей действительной оси, то на основании теоремы (12.1.15) его можно почленно дифференцировать, в результате чего получим разложение 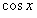 в степенной ряд
в степенной ряд
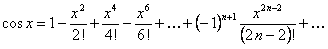
или
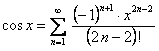 .(12.1.59)
.(12.1.59)
Отметим, что 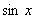 (нечетная функция) разлагается по нечетным степеням
(нечетная функция) разлагается по нечетным степеням 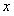 , а
, а 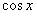 (четная функция) – по четным степеням
(четная функция) – по четным степеням 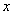 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >