Разложение функций в ряды Маклорена позволяет во многих случаях вычислять с большой точностью значения этих функций.
ПРИМЕР 12.1.20 Вычислить с точностью до пяти знаков 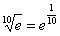 .
.
Решение. Воспользуемся разложением 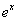 , положив
, положив 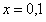
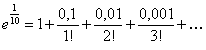 . Значит,
. Значит, 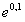 близко к единице. Остаточный член
близко к единице. Остаточный член 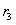 имеет вид
имеет вид
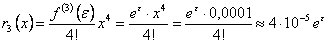 , где
, где 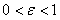 , так что
, так что 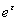 близко к единице. Поэтому ненаписанные члены в разложении
близко к единице. Поэтому ненаписанные члены в разложении 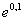 не повлияют на первые пять знаков после запятой, их можно отбросить.
не повлияют на первые пять знаков после запятой, их можно отбросить.
Тогда 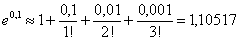 .
.
Иногда при вычислении значений функций удобно пользоваться почленным дифференцированием или интегрированием рядов.
ПРИМЕР 12.1.21 Вычислить 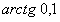 .
.
Решение. В разложении (12.1.70), заменив 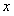 на
на 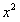 , получим
, получим
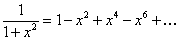 (12.1.73)
(12.1.73)
Ряд сходится равномерно при 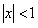 , поэтому его можно почленно интегрировать. Выполнение этого интегрирования от
, поэтому его можно почленно интегрировать. Выполнение этого интегрирования от 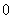 до
до 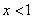 нам дает
нам дает
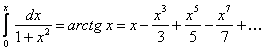 (12.1.74)
(12.1.74)
В частности, при 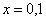 имеем
имеем
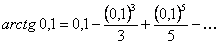 (12.1.75)
(12.1.75)
Полученный ряд знакочередующийся. Поэтому его остаток не превосходит по абсолютной величине первого из отброшенных членов. Сохраняя в (12.1.75) два первых члена, получим, что 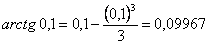 с пятью верными знаками.
с пятью верными знаками.
При помощи биномиального ряда можно вычислить значения корней из чисел, а также значений различных функций.
ПРИМЕР 12.1.22 Вычислить 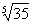 с точностью до
с точностью до 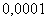 .
.
Решение. Представим 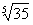 в следующем виде:
в следующем виде:
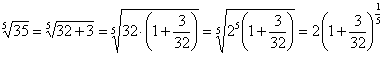 .
.
Отсюда 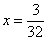 , а
, а 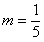 . Воспользуемся разложением в ряд, то есть разложением (12.65), тогда
. Воспользуемся разложением в ряд, то есть разложением (12.65), тогда 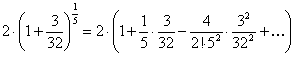 .
.
Получили числовой знакочередующийся ряд. По условию 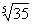 нужно вычислить с точностью до
нужно вычислить с точностью до 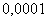 , поэтому все члены, которые по абсолютной величине меньше
, поэтому все члены, которые по абсолютной величине меньше 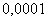 , можно отбросить. Проверим четвертый член
, можно отбросить. Проверим четвертый член
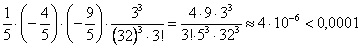 .
.
Значит, 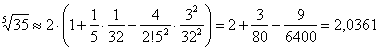 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >