Пусть функция 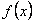 (периодическая, с периодом
(периодическая, с периодом 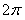 ) удовлетворяет условиям теоремы Дирихле.
) удовлетворяет условиям теоремы Дирихле.
Если функция 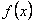 четная, то произведение
четная, то произведение 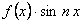 нечетная:
нечетная:
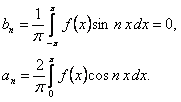 (12.1.106)
(12.1.106)
Таким образом, ряд Фурье четной функции содержит лишь косинусы:
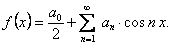
Если 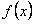 нечетная, то произведение
нечетная, то произведение 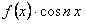 нечетная:
нечетная:
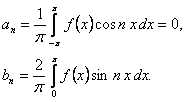 (12.1.107)
(12.1.107)
Отсюда следует, что ряд Фурье нечетной функции содержит одни лишь синусы:
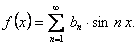
ПРИМЕР 12.1.28 Разложить в ряд Фурье функцию 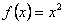 периода
периода 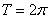
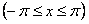 . Данная функция четная. Тогда ее ряд Фурье содержит только косинусы
. Данная функция четная. Тогда ее ряд Фурье содержит только косинусы 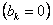 . Вычислим коэффициенты
. Вычислим коэффициенты 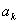 :
:
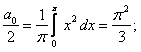
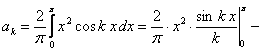
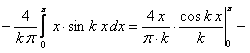
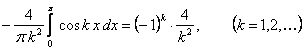 .
.
Таким образом, 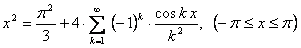 .
.
ПРИМЕР 12.1.29 Периодическая с периодом 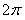 функция
функция 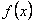 определена следующим образом:
определена следующим образом: 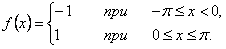
Эта функция нечетная. Тогда ее ряд Фурье содержит только синусы 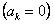 . Вычислим коэффициент
. Вычислим коэффициент 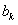 :
:
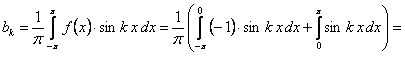
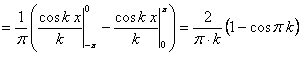 .
.
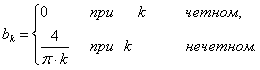
Следовательно, для рассматриваемой функции ряд Фурье имеет вид
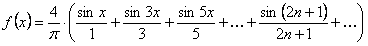 .
.
Это равенство справедливо во всех точках, кроме точек разрыва.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >