Пусть 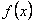 есть периодическая функция с периодом
есть периодическая функция с периодом 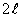 . Разложим ее в ряд Фурье. Сделаем замену переменной по формуле
. Разложим ее в ряд Фурье. Сделаем замену переменной по формуле
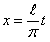 .
.
Тогда функция 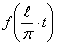 будет периодической функцией от
будет периодической функцией от 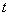 с периодом
с периодом 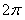 .
.
Ее можно разложить в ряд Фурье на отрезке 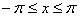 :
:
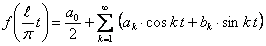 (12.1.106)
(12.1.106)
где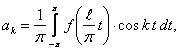
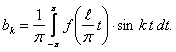
Переходим к старой переменной 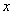 :
: 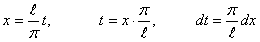 .
.
Тогда получим
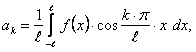 (12.1.107)
(12.1.107)
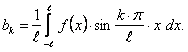 (12.1.108)
(12.1.108)
Равенство (1) примет вид
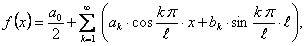 (12.1.109)
(12.1.109)
где коэффициенты 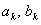 вычисляются по формулам (12.1.107), (12.1.108). Все утверждения, которые имели место для рядов Фурье от периодических функций с периодом
вычисляются по формулам (12.1.107), (12.1.108). Все утверждения, которые имели место для рядов Фурье от периодических функций с периодом 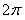 , сохраняются и для рядов Фурье от периодических функций с периодом
, сохраняются и для рядов Фурье от периодических функций с периодом 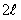 .
.
ПРИМЕР 12.1.29 Разложить в ряд Фурье периодическую функцию 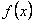 с периодом
с периодом 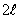 , которая на отрезке
, которая на отрезке 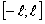 задается равенством
задается равенством
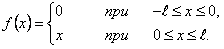
Определим коэффициенты Фурье
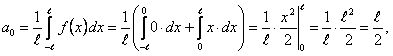
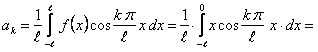
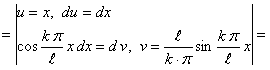
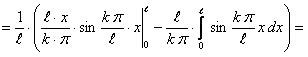
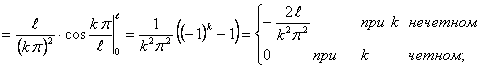
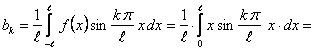
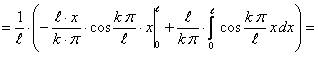
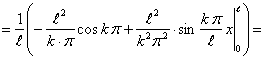
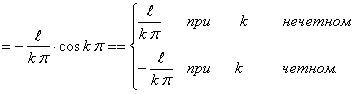
Таким образом, ряд Фурье для этой функции будет иметь вид
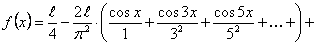
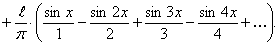
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >