Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения, кроме дисперсии, служат и некоторые другие характеристики, например, среднее квадратическое отклонение.
Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: 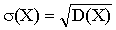 .
.
Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то размерность 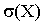 совпадает с размерностью X.
совпадает с размерностью X.
Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию.
Например, если Х выражается в метрах, то 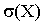 будет выражаться также в метрах, a
будет выражаться также в метрах, a 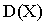 — в квадратных метрах.
— в квадратных метрах.
ПРИМЕР 13.1.39 Случайная величина Х задана законом распределения
| X | 0 | 5 | 10 | 15 |
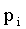 |
0,2 | 0,4 | 0,3 | 0,1 |
Найти среднее квадратическое отклонение 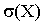 .
.
Решение. Найдем математическое ожидание M(X) и дисперсию D(X):
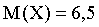 ,
, 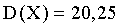 .
.
Тогда 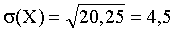 .
.
Онлайн помощь по математике
Лекции по высшей математике
Примеры решения задач