Пусть непрерывная случайная величина Х задана плотностью распределения f(х). Допустим, что все возможные значения X принадлежат отрезку [а;b]. Разобьем этот отрезок на п частичных отрезков длиной 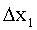, , 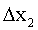…, 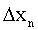и выберем в каждом из них произвольную точку 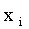( i=1, 2, …, n).

Определим математическое ожидание непрерывной величины по аналогии с дискретной; составим сумму произведений возможных значений 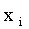, на вероятности попадания их в интервал :

.

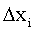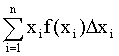Перейдя к пределу, получим определенный интеграл

.

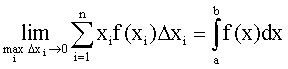Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а;b], называют определенный интеграл

.

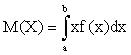Если возможные значения принадлежат всей оси Ох, то

.

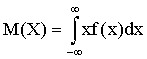Предполагается, что несобственный интеграл сходится абсолютно, т, е. существует интеграл 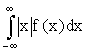. Если бы это требование не выполнялось, то значение интеграла зависело бы от скорости стремления (в отдельности) нижнего предела к 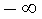, а верхнего — к 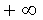.По аналогии с дисперсией дискретной величины определяется и дисперсия непрерывной величины.

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения Х принадлежат отрезку [а;b], то
,

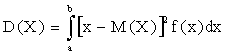если же возможные значения распределены по всей оси Ox, то
.

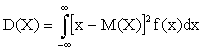Среднее квадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством
.

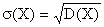Замечание 1. Можно доказать, что свойства математического ожидания и дисперсии дискретных величин сохраняются и для непрерывных величин.

Замечание 2. Легко получить для вычисления дисперсии более удобные формулы:

,

.

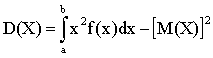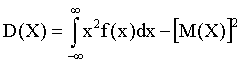ПРИМЕР 13.1.45 Найти математическое ожидание и дисперсию непрерывной случайной величины X, распределенной равномерно в интервале (a;b):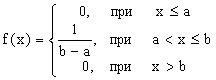

Решение. Найдем математическое ожидание Х по формуле .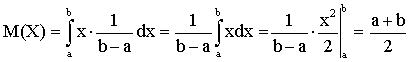

Найдем дисперсию Х по формуле .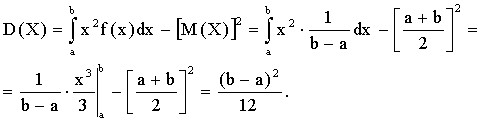

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >