Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
Пример. Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при округлении отсчета до ближайшего целого деления можно рассматривать как случайную величину X, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Таким образом, X имеет равномерное распределение.
Найдем плотность равномерного распределения f(x), считая, что все возможные значения случайной величины заключены в интервале (a;b), на котором функция f (х) сохраняет постоянные значения.
По условию Х не принимает значений вне интервала (a;b), поэтому
f(х)=0 при x < a и x > b.
Найдем постоянную С. Так как все возможные значения случайной величины принадлежат интервалу (a;b), то должно выполняться соотношение
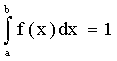
или
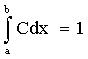 .
.
Отсюда 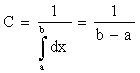 .
.
Итак, искомая плотность вероятности равномерного распределения f(x):
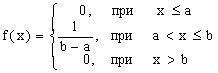 .
.
Далее легко получить 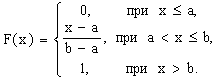
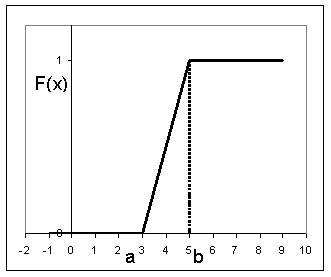
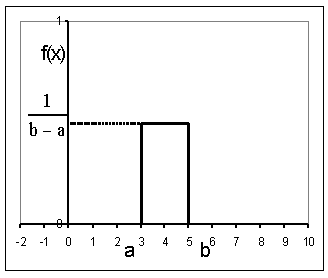
График функции равномерного распределения изображен на рис.13.1.24, а график плотности распределения — на рис.13.1.25.
 |
 |
|
Рис.13.1.24
|
Рис.13.1.25
|
Как было показано ранее, для равномерного распределения
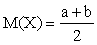 ,
, 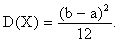
ПРИМЕР 13.1.49 Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени, никак не связанный с расписанием поездов. Найти вероятность того, что ему придется ждать не более полминуты.
Решение.
По условию 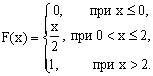
Тогда искомая вероятность 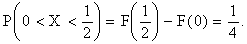
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >