Важной характеристикой условного распределения вероятностей является условное математическое ожидание.
Условным математическим ожиданием дискретной случайной величины Y при X = x (x – определенное возможное значение X) называют произведение возможных значений Y на их условные вероятности:
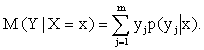 (13.1.50)
(13.1.50)
Для непрерывных величин
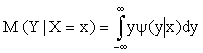 ,
,
где 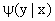 — условная плотность случайной величины Y при X = x.
— условная плотность случайной величины Y при X = x.
Условное математическое ожидание M (Y | x) есть функция от x:
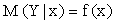 ,
,
которую называют функцией регрессии Y на X.
Аналогично определяются условное математическое ожидание случайной величины X и функция регрессии X на Y: 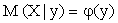 .
.
ПРИМЕР 13.1.58 Дискретная двумерная случайная величина задана таблицей
| Y\X | 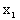 |
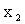 |
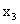 |
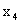 |
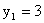 |
0,15 | 0,06 | 0,25 | 0,04 |
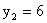 |
0,30 | 0,10 | 0,03 | 0,07 |
Найти условное математическое ожидание составляющей Y при 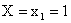 .
.
Решение. Найдем 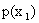 , для чего сложим вероятности, помещенные в первом столбце таблицы:
, для чего сложим вероятности, помещенные в первом столбце таблицы:
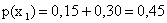 .
.
Найдем условное распределение вероятностей величины Y при 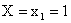 :
:
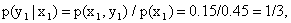 ,
,
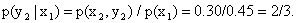
Найдем искомое условное математическое ожидание по формуле (13.1.50):
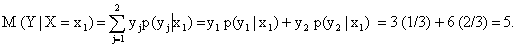
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >