Две случайные величины X и Y называют коррелированными, если их корреляционный момент (коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю.
Две коррелированные величины также и зависимы. Действительно, допустив противное, мы должны заключить, что 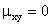 , а это противоречит условию, так как для коррелированных величин
, а это противоречит условию, так как для коррелированных величин 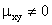 .
.
Обратное предположение не всегда имеет место, т. е. если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равен нулю, но может и равняться нулю.
Убедимся на примере, что две зависимые величины могут быть некоррелированными.
ПРИМЕР 13.1.60 Двумерная случайная величина (X, Y) задана плотностью распределения:

Доказать, что X и Y — зависимые некоррелированные величины.
Решение. Воспользуемся ранее вычисленными плотностями распределения составляющих X и Y (см. пример прим.13.1.55):
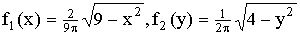 внутри заданного эллипса и
внутри заданного эллипса и
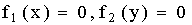 вне его.
вне его.
Так как 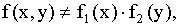 , то X и Y — зависимые величины.
, то X и Y — зависимые величины.
Для того, чтобы доказать некоррелированность X и Y , достаточно убедиться в том, что 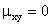 . Найдем корреляционный момент
. Найдем корреляционный момент
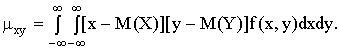 .
.
Поскольку функция 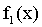 симметрична относительно оси Oy, то M(X)=0; аналогично M(Y)=0 в силу симметрии
симметрична относительно оси Oy, то M(X)=0; аналогично M(Y)=0 в силу симметрии 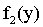 относительно оси Ox. Следовательно,
относительно оси Ox. Следовательно,
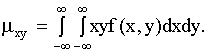 .
.
Вынося постоянный множитель f(x,y) за знак интеграла, получим
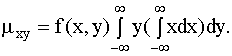 .
.
Внутренний интеграл равен нулю (подынтегральная функция нечетна, пределы интегрирования симметричны относительно начала координат), следовательно, 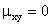 , т.е. зависимые случайные величины X и Y некоррелированы.
, т.е. зависимые случайные величины X и Y некоррелированы.
Итак, из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух величин следует их коррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.
Заметим, однако, что из некоррелированности нормально распределенных величин вытекает их независимость. Это утверждение доказывается в следующем разделе.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >