Если каждому возможному значению случайной величины X соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента X и записывают 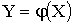 .
.
Рассмотрим правила для нахождения закона распределения СВ Y по известному закону распределения СВ X.
Пусть аргумент X — дискретная случайная величина, с законом распределения:
| X | 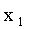 |
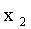 |
… | 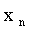 |
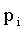 |
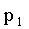 |
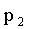 |
… | 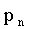 |
Если различным значениям СВ X соответствуют различные значения СВ Y, то вероятности соответствующих значений равны; если же различным значениям СВ X соответствуют значения СВ Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y.
Математическое ожидание функции
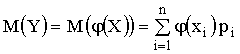 .
.
Пусть аргумент X — непрерывная случайная величина, заданная плотностью распределения 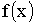 .
.
Если функция 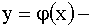 дифференцируемая строго монотонная, обратная функция которой
дифференцируемая строго монотонная, обратная функция которой 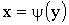 , то плотность распределения
, то плотность распределения 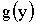 случайной величины Y находится по формуле
случайной величины Y находится по формуле
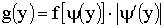 .
.
Если функция 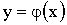 в интервале возможных значений X не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция
в интервале возможных значений X не монотонна, то следует разбить этот интервал на такие интервалы, в которых функция 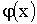 монотонна, и найти плотности распределений
монотонна, и найти плотности распределений 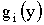 для каждого из интервалов монотонности, а затем представить в виде суммы
для каждого из интервалов монотонности, а затем представить в виде суммы 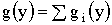 .
.
Например, если функция 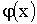 монотонна в двух интервалах, в которых соответствующие обратные функции равны
монотонна в двух интервалах, в которых соответствующие обратные функции равны 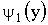 и
и 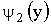 , то
, то
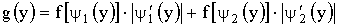
Математическое ожидание и дисперсия функции непрерывного случайного аргумента 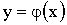
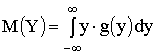 ,
,
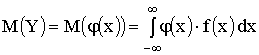
или
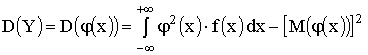 .
.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
ПРИМЕР 13.2.45. Дискретная случайная величина задана законом распределения
| X | -1 | 0 | 1 | 2 |
| P | 0,1 | 0,2 | 0,4 | 0,3 |
Найти закон распределения случайной величины 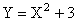 и ее математическое ожидание.
и ее математическое ожидание.
Решение. Найдем возможные значения Y:
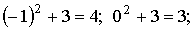 .
.
Возможному значению Y=4, соответствуют возможные значения X=-1 и X=1, поэтому 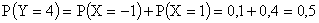 . Вероятности возможных значений
. Вероятности возможных значений 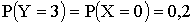
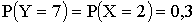
Итак, искомый закон распределения функции
| Y | 3 | 4 | 7 |
| P | 0,2 | 0,5 | 0,3 |
ПРИМЕР 13.2.46. Дана нормально распределенная случайная величина X с 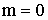 и
и 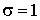 . Найти закон распределения СВ
. Найти закон распределения СВ 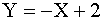 .
.
Решение. По условию задачи 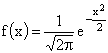 .
.
Так как 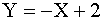 , то
, то 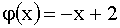 . Найдем для
. Найдем для 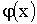 обратную функцию
обратную функцию 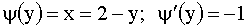 . Тогда плотность распределения случайной величины Y будет иметь вид
. Тогда плотность распределения случайной величины Y будет иметь вид 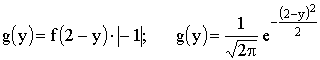 .
.
ПРИМЕР 13.2.47. Нормально распределенная случайная величина X имеет плотность 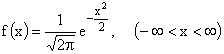 .
.
Найти плотность распределения 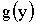 случайной величины
случайной величины 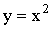 .
.
Решение. Функция 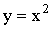 на
на 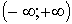 не монотонна. Интервалы монотонности
не монотонна. Интервалы монотонности 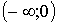 и
и 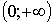 . На интервале
. На интервале 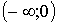 обратная функция
обратная функция 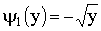 ;
; 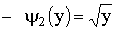 на
на 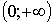 ;
;
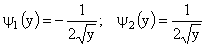 .
.
Тогда
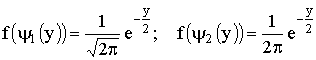
или 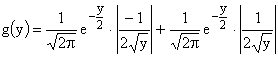 .
.
Так как 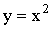 , причем
, причем 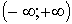 , то
, то 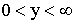 .
.
Таким образом 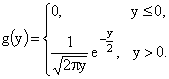
ПРИМЕР 13.2.48. Случайная величина задана плотностью
Найти математическое ожидание случайной величины 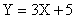 .
.
Решение. I способ: Найдем 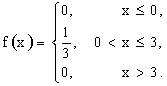 .
.
По свойствам математического ожидания 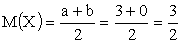
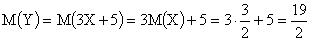 .
.
II способ: Воспользуемся формулой 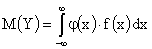 . Тогда,
. Тогда, 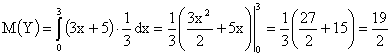 .
.
Примеры и задачи для самостоятельного решения
Решить задачи, используя формулы расчета вероятности для функции одного случайного аргумента
3.2.10.1. Дискретная случайная величина X задана законом распределения
| X | 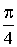 |
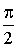 |
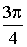 |
| P | 0,2 | 0,7 | 0,1 |
Найти закон распределения случайной величины 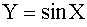 и ее математическое ожидание.
и ее математическое ожидание.
Отв.:
| Y | 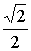 |
1 |
| P | 0,3 | 0,7 |
3.2.10.2. Случайная величина X равномерно распределена в интервале 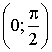 . Найти плотность распределения g(y) случайной величины
. Найти плотность распределения g(y) случайной величины 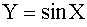 .
.
Отв.: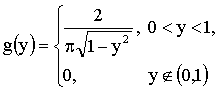
3.2.10.3. Задана плотность распределения f(x) случайной величины X: 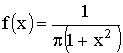 . Найти плотность распределения случайной величины
. Найти плотность распределения случайной величины 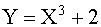 .
.
Отв.: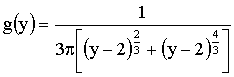
3.2.10.4. Ребро куба x измерено приближенно, причем 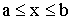 . Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию объема куба .
. Рассматривая ребро куба как случайную величину X, распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию объема куба .
Отв.: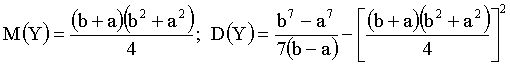
5. Диаметр круга x измерен приближенно, причем 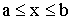 . Рассматривая диаметр как случайную величину X, распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию площади круга.
. Рассматривая диаметр как случайную величину X, распределенную равномерно в интервале (a,b), найти математическое ожидание и дисперсию площади круга.
Отв.: 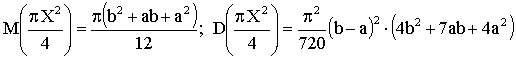
3.2.10.6. Случайная величина X распределена равномерно в интервале 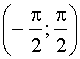 . Найти плотность распределения g(y) случайной величины
. Найти плотность распределения g(y) случайной величины 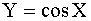 .
.
Отв.:
3.2.10.7. Задана плотность распределения f(x) случайной величины X, возможные значения которой заключены в интервале 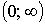 . Найти плотность распределения g(y) случайной величины Y, если: а)
. Найти плотность распределения g(y) случайной величины Y, если: а) 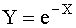 ; б)
; б) 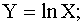 в)
в) 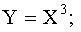 г)
г) 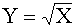 .
.
Отв.: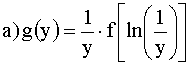 , б)
, б)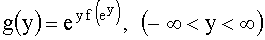 ,
,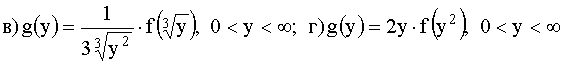
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >