Статистической гипотезой называется любое предположение относительно закона распределения исследуемой случайной величины .

Гипотезы бывают простые и сложные. Простая гипотеза полностью определяет закон распределения величины в отличие от сложной.

Гипотезы бывают параметрическими и непараметрическими. В первом случае мы имеем предположение о параметрах распределения при известном законе, а во втором – о самом виде закона распределения.

Пример 14.1.2. Гипотеза о том, что математическое ожидание нормальной величины равно при условии, что дисперсия известна, является простой параметрической. Если же дисперсия неизвестна, то гипотеза будет сложной параметрической.

Пример 14.1.3. Гипотеза о том, что случайная величина распределена по нормальному (или по какому-то другому) закону, является сложной непараметрической.

Наряду с выдвинутой гипотезой рассматривают противоречащую ей гипотезу . Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая ей гипотеза .

Критерием проверки статистической гипотезы называется некоторое правило, позволяющее принять ее или отвергнуть. Причем критерии строятся с помощью случайной величины (часто именно ее называют критерием), для которой известно распределение. Наблюдаемым значением критерия называют значение критерия, вычисленное по данным выборки.

В случае проверки гипотез возможны ошибки:

Ошибка 1-го рода состоит в том, что будет отвергнута правильная гипотеза. Вероятность ошибки первого рода называется уровнем значимости критерия, по которому производится проверка.

Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза. Если — вероятность ошибки второго рода, то величина называется мощностью критерия.

Параметрические гипотезы проверяются с помощью критериев значимости, а непараметрические – с помощью критериев согласия.

Критической областью называется совокупность значений критерия, при которых нулевую гипотезу отвергают. Если уровень значимости уже выбран и задан объем выборки, то критическую область следует строить так, чтобы мощность критерия была максимальной. Выполнение этого требования должно обеспечить минимальную ошибку второго рода, что более желательно.

Основной принцип проверки статистических гипотез: если принадлежит критической области – гипотезу отвергают, если же принадлежит области принятия гипотезы, то гипотезу принимают.

Остановимся только на гипотезе о законе распределения генеральной совокупности.

В 14.1.2 при группировке данных выборочной совокупности получена табл. 14.1.4 – эмпирический закон распределения выборки и по данным этой таблицы построен полигон относительных частот. Относительные частоты иногда называют эмпирическими вероятностями. Из визуального наблюдения ломаной полигона делается вывод (выдвигается гипотеза ) о законе распределения:

: генеральная совокупность распределена по нормальному закону.

И выдвигается гипотеза, противоречащая гипотезе или ее отвергающая.

Проверка гипотезы о предполагаемом законе неизвестного распределения производится при помощи специально подобранной случайной величины – критерия согласия. Разработано несколько таких критериев: — Пирсона, Колмогорова, Смирнова и др. Рассмотрим критерий — Пирсона, как классический пример применительно к проверке гипотезы о нормальном распределении генеральной совокупности.

Будем сравнивать эмпирические и теоретические вероятности. Обычно они различаются. Случайно ли это расхождение? Возможно, что расхождение случайно (незначимо) и объясняется либо малым числом исходных данных, либо способом их группировки или другими причинами. Возможно, что данное расхождение неслучайно (значимо) и объясняется тем, что теоретические вероятности вычислены исходя из неверной гипотезы о нормальном распределении генеральной совокупности.

Пусть нам задан уровень значимости ( — доверительная вероятность, то есть вероятность принять верную гипотезу; — это вероятность отвергнуть верную гипотезу, причем ). Для того, чтобы при заданном проверить гипотезу о нормальном распределении генеральной совокупности, надо вычислить теоретические вероятности. Плотность распределения для нормального закона есть функция:

. (14.1.12)

Тогда, пользуясь формулой нахождения вероятности попадания случайной величины в интервал:

,

имеем для всех :

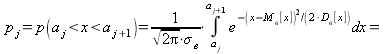
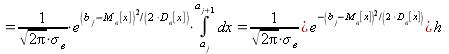,(14.1.13)

где — границы частичных подынтервалов (см. 14.1.2);

— середина го частичного подынтервала;

— длина частичного подынтервала (см. формулу (14.1.2)).

Составляется сводная таблица на основе данных табл. 14.1.4 и рассчитанных теоретических вероятностей:

Таблица 14.1.5

			…		…
			…		…		эмпирические вероят.
			…		…		теоретические вероят.

Оценка отклонения эмпирических вероятностей от теоретических вероятностей производится с помощью критерия Пирсона :

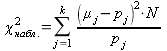. (14.1.14)

По таблице критических точек распределения (приложения 4) по заданному уровню значимости и числу степеней свободы ( — количество подынтервалов) находим критическое значение правосторонней критической области.

Правило 1.1. Если , тогда нет оснований отвергать гипотезу о нормальном распределении генеральной совокупности (то есть эмпирические и теоретические частоты различаются незначимо (случайно)).

Правило 1.2. Если , тогда гипотеза отвергается.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >