Если в уравнении 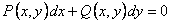не выполнено условие, 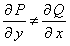, то это уравнение не является уравнением в полных дифференциалах. Возникает вопрос, нельзя ли такое уравнение умножением на подходящий множитель 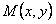превратить в уравнение в полных дифференциалах.

Иногда удается подобрать такой множитель 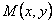, который называется интегрирующим множителем.

Для того, чтобы функция 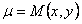была интегрирующим множителем, нужно, чтобы выражение 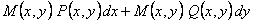было полным дифференциалом. Необходимым и достаточным условием этого является равенство .

Онлайн помощь

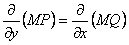Выполняя дифференцирование, мы приходим к соотношению

.

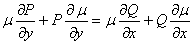Это соотношение содержит неизвестную функцию 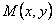и ее частные производные, представляя, таким образом, так называемое уравнение в частных производных. Решение его, вообще говоря, составляет задачу более сложную, чем решение исходного уравнения.

Нахождение интегрирующего множителя проводится сравнительно просто, когда он является функцией одной переменной: либо 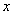, либо .

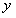ТЕОРЕМА 11.1.3 Необходимым и достаточным условием того, чтобы дифференциальное уравнение 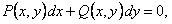имело интегрирующий множитель, зависящий от 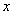, является требование, чтобы выражение 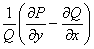было функцией только от x. В этом случае интегрирующий множитель выражается в квадратурах и может быть найден по формуле

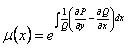.(11.1.14)

Доказательство теоремы опускаем.

Аналогично, если 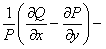функция, зависящая только от 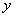, то дифференциальное уравнение имеет интегрирующий множитель .

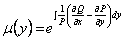ПРИМЕР 11.1.18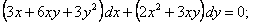

Решение.

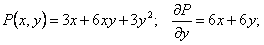
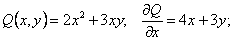видно, что 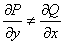. Теперь найдем выражение .

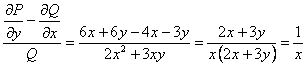Следовательно, .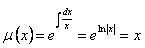

Умножая данное уравнение на x, получаем уравнение в полных дифференциалах

.

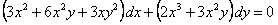Далее находим общий интеграл по формуле

, .

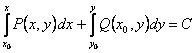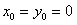Тогда 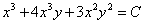общий интеграл этого уравнения.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >