Функции 
являются решениями уравнения
(11.1.27)
на интервале 
.
ТЕОРЕМА 11.1.11 Если 
— два линейно независимых решения уравнения (11.1.27), то
, (11.1.28)
где 
произвольные постоянные, является его общим решением.
Доказательство. Из свойств решения уравнения (11.1.27) следует, что функция 
является его решением.
Докажем, что каковы бы ни были начальные условия 
, 
, можно так подобрать значения произвольных постоянных 
, чтобы соответствующее частное решение 
удовлетворяло заданным начальным условиям.
Подставляя начальные условия в равенство (11.1.28), имеем
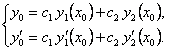(11.1.29)
Система уравнений (11.1.29) имеет единственное решение так, как главный определитель этой системы
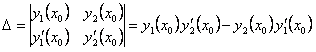
есть определитель Вронского при 
отличен от нуля согласно теоремы 11.10. Частное решение, которое получается из решения (11.1.28) при найденных значениях 
удовлетворяет начальным условиям. Таким образом, теорема доказана.
ПРИМЕР 11.1.24 Написать общее решение дифференциального уравнения
, если 
его частные решения.
Решение.
Функции 
линейно независимы, согласно теоремы 11.11, поэтому 
является его общим решением.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
