ОПРЕДЕЛЕНИЕ 11.1.19 Линейной системой дифференциальных уравнений с постоянными коэффициентами второго порядка называется система вида
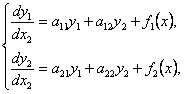 (11.1.52)
(11.1.52)
где 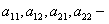 постоянные,
постоянные, 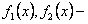 непрерывные функции на интервале
непрерывные функции на интервале  .
.
ОПРЕДЕЛЕНИЕ 11.1.20 Линейная система называется однородной, если 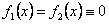 на интервале
на интервале  , то есть система имеет вид
, то есть система имеет вид
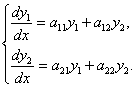 (11.1.53)
(11.1.53)
Решения системы будем искать в виде
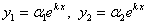 , (1.1.54)
, (1.1.54)
где 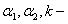 постоянные.
постоянные.
Подставляя в систему (11.1.53) функции 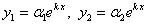 , сокращая на
, сокращая на 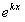 и перенося все члены в одну часть равенства, получим
и перенося все члены в одну часть равенства, получим
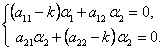 (11.1.55)
(11.1.55)
Для того, чтобы эта система линейных однородных уравнений с двумя неизвестными 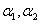 имела ненулевое решение, необходимо и достаточно, чтобы главный определитель системы (11.1.55) был равен нулю:
имела ненулевое решение, необходимо и достаточно, чтобы главный определитель системы (11.1.55) был равен нулю:
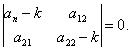 (11.1.56)
(11.1.56)
Уравнение (11.1.56) называется характеристическим для системы (11.1.53), его корни называются корнями характеристического уравнения.
1. Корни характеристического уравнения действительные и различные. Обозначим через 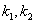 корни характеристического уравнения. Для каждого корня
корни характеристического уравнения. Для каждого корня 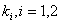 напишем систему (11.1.55) и определим коэффициенты
напишем систему (11.1.55) и определим коэффициенты 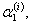
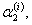
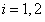 .
.
Можно показать, что один из них произвольный, так как система (11.1.55) однородная, его можно считать равным единице. Таким образом, получаем:
для корня 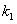 решение системы (11.1.53)
решение системы (11.1.53) 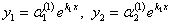 ;
;
для корня 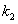 решение системы (11.1.53)
решение системы (11.1.53) 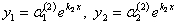 .
.
Тогда можно показать, что функции 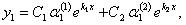
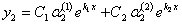 являются общим решением системы (11.1.53), где
являются общим решением системы (11.1.53), где 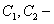 произвольные постоянные.
произвольные постоянные.
ПРИМЕР 11.1.31 Найти общее решение системы 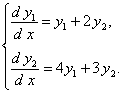
Решение.
Составляем характеристическое уравнение 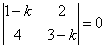 или
или 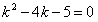 , которое имеет корни
, которое имеет корни 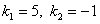 .
.
Для определения чисел 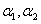 подставляем в систему (11.1.55) значение
подставляем в систему (11.1.55) значение 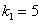 , получаем
, получаем 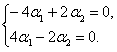 Решая ее, находим
Решая ее, находим 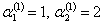 , тогда
, тогда 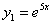 ,
, 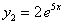 .
.
Подставляя в систему значение 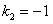 , решая полученную систему, имеем
, решая полученную систему, имеем 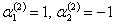 и
и 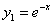 ,
, 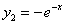 .
.
Следовательно, функции 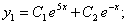
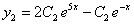 являются общим решением системы.
являются общим решением системы.
2. Корни характеристического уравнения комплексные. Эти корни обозначим через 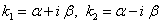 . Этим корням будут соответствовать решения
. Этим корням будут соответствовать решения 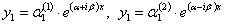 ;
;
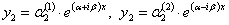 .
.
Коэффициенты 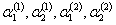 определяются из системы уравнений (11.1.55).
определяются из системы уравнений (11.1.55).
Можно показать, что действительные и мнимые части комплексного решения также являются решениями. Таким образом, получаем частные решения:
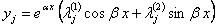 ,
,
где 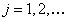 ,
, 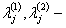 действительные числа, определяемые через
действительные числа, определяемые через 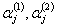 .
.
На основе этих частных решений можно написать общее решение.
ПРИМЕР 11.1.32 Найти общее решение системы дифференциальных уравнений 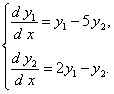
Решение.
Характеристическое уравнение 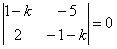 или
или 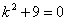 имеет корни
имеет корни 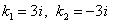 . Решения этой системы имеют вид:
. Решения этой системы имеют вид: 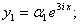
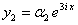 , подставляя
, подставляя 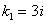 в систему (11.1.55), находим
в систему (11.1.55), находим 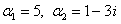 . Следовательно,
. Следовательно, 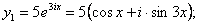
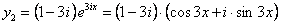 . Действительная и мнимая части этих функций также являются решениями системы, а их линейная комбинация с произвольными постоянными
. Действительная и мнимая части этих функций также являются решениями системы, а их линейная комбинация с произвольными постоянными 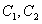 является общим решением системы:
является общим решением системы: 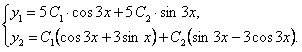
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >