Уравнение вида 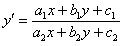 при
при 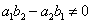 приводится к однородному подстановкой
приводится к однородному подстановкой 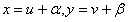 , где
, где 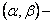 точки пересечения прямых
точки пересечения прямых 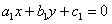 и
и 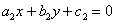 .
.
Если же 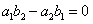 , то подстановкой
, то подстановкой 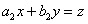 уравнение приводится к уравнению с разделяющимися переменными.
уравнение приводится к уравнению с разделяющимися переменными.
ПРИМЕР 11.2.29 Найти общий интеграл уравнения 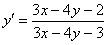 .
.
Решение.
Составим определитель из коэффициентов при 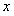 и y
и y 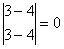 . Так как определитель равен нулю, то данное уравнение приводится к уравнению с разделяющимися переменными подстановкой
. Так как определитель равен нулю, то данное уравнение приводится к уравнению с разделяющимися переменными подстановкой 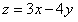 ,
, 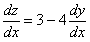 откуда
откуда 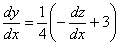 . Подставим в данное уравнение, получим
. Подставим в данное уравнение, получим 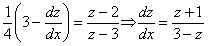 . Разделяя переменные и интегрируя, имеем
. Разделяя переменные и интегрируя, имеем 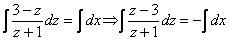 .
.
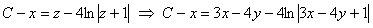
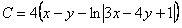 или
или 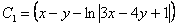 , где
, где 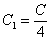 .
.
ПРИМЕР 11.2.30 Найти общее решение уравнения 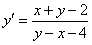 .
.
Решение.
Вычислим определитель, составленный из коэффициентов при x и y
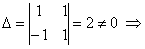 данное уравнение, приводится к однородному. Сделаем подстановку
данное уравнение, приводится к однородному. Сделаем подстановку 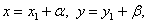 тогда
тогда 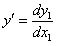 и подставим в данное уравнение
и подставим в данное уравнение
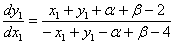 (*)
(*)
Неизвестные 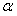 и
и 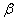 находим из системы
находим из системы
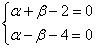 (**) Решая систему, получим
(**) Решая систему, получим 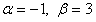 . При условии (**) уравнение (*) примет вид
. При условии (**) уравнение (*) примет вид
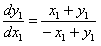 (***) Уравнение (***) является однородным. Сделаем подстановку
(***) Уравнение (***) является однородным. Сделаем подстановку 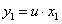 ,
, 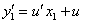 подставим в уравнение (***)
подставим в уравнение (***)
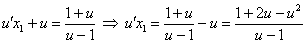 .
.
Разделяя переменные и интегрируя, получим
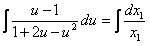 или
или 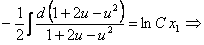
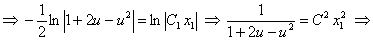
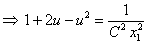 . Так как
. Так как 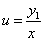 , то последнее уравнение примет вид
, то последнее уравнение примет вид 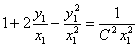
или 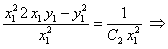
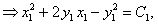 (****) где
(****) где 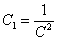 . В уравнение (****) подставим
. В уравнение (****) подставим 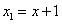 и
и 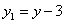 , получим
, получим 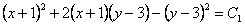 или
или 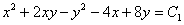 .
.
Примеры и задачи для самостоятельного решения
| Решить уравнения | |
11.2.31 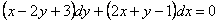 |
Отв.: 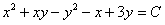 |
11.2.32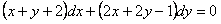 |
Отв.: 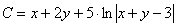 |
11.2.33 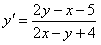 |
Отв.: 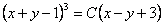 |
11.2.34 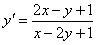 |
Отв.: 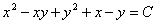 |
11.2.35 Найти интегральную кривую дифференциального уравнения 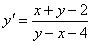 , проходящую через точку M(1;1) , проходящую через точку M(1;1) |
Отв.: 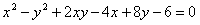 . . |
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >