ОПРЕДЕЛЕНИЕ 11.2.20 Линейным дифференциальным уравнением с переменными коэффициентами называется уравнение вида

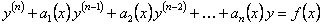. (11.2.11)

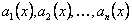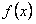В уравнении (11.2.11) и заданы и непрерывны в некотором интервале .

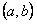Если 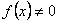, то уравнение (10.1) называется неоднородным или с правой частью.

Если 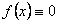, то уравнение называется однородным.

Зная одно частное решение 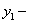линейного однородного уравнения, можно с помощью замены 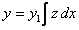понизить порядок уравнения на единицу.

ТЕОРЕМА 11.2.2 (о структуре общего решения линейного однородного уравнения)

Если 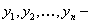линейно независимые частные решения уравнения

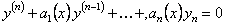,                       (11.2.12)

то

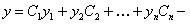            (11.2.13)

общее решение этого уравнения .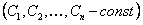

В частности для уравнения 2-го порядка

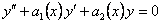          (11.2.14) общее решение имеет вид

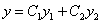,                (11.2.15) где 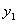и 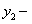два частных линейных независимых решения.

ОПРЕДЕЛЕНИЕ 11.2.21 Две функци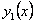и и 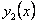называются линейно независимыми, если их отношение не является постоянной величиной, т.е. .

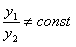Необходимым и достаточным условием линейной независимости двух функций непрерывных вместе со своими производными до первого порядка в интервале является то, что определитель Вронского (вронскиан) 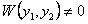ни в одной точки интервала 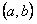, т.е.

.

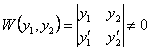Если для уравнения (11.2.13) известно одно частное решение 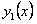, то второе его решение, линейно независимое с первым, можно найти по формуле

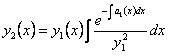.    (11.2.14)

Формула (11.2.14) дает возможность интегрировать линейные однородные уравнения 2-го порядка, сразу, не прибегая к понижению их порядка.

ПРИМЕР 11.2.93 Решить уравнение 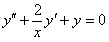двумя способами:

1) путем понижения порядка; 2) по формуле (11.2.14).

Решение.

1) Пусть известно одно частное решение данного уравнения 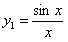. Произведем замену 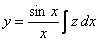; тогда

.

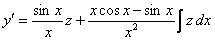
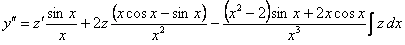Подставляя в уравнение, получим: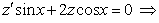

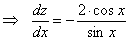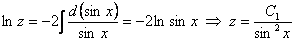; . Следовательно,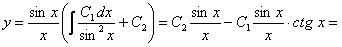

.

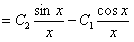2) Решим данное уравнение, применяя формулу (11.2.14)

.

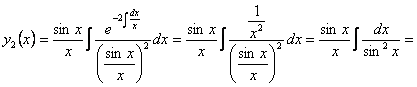
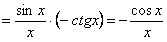Общее решение, по теореме о структуре будет иметь вид

.

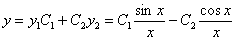Примеры и задачи для самостоятельного решения

11.2.94 Понизить порядок и проинтегрировать уравнение 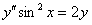, имеющее частное решение .

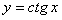Отв.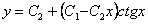

11.2.95 Уравнение 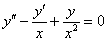имеет частное решение y=x. Понизить порядок и проинтегрировать это уравнение.

Отв.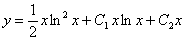

11.2.96 Уравнение 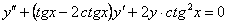имеет частное решение y=sinx. Понизить порядок и проинтегрировать это уравнение.

Отв.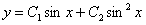

11.2.97 Подобрав одно частное решение уравнения, найти обще решение .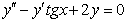

Отв.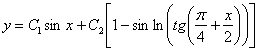

11.2.98 Подобрав одно частное решение уравнения, найти общее решение .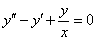

Отв.

11.2.99 Показать, что 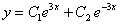является общим решением уравнения .

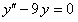11.2.100 Уравнению 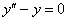удовлетворяют два частных решения 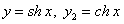. Составляют ли они фундаментальную систему?

11.2.101 Можно ли составить общее решение уравнения 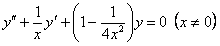по двум его частным решениям ?

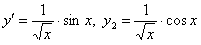Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >