Вероятность события A определяется формулой

,

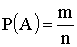где m-число элементарных исходов, благоприятствующих событию A ;

n-число всех возможных элементарных исходов испытания.

Предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПРИМЕР 13.2.16. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.

Решение: Введем события: 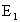– одно очко; 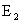— два очка; 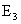– три очка; 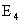– четыре очка; 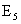– пять очков; 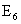– шесть очков. Итак, n=6.

Рассмотрим событие A — выпадение четного числа очков. Данному событию благоприятствуют элементарные исходы , , .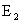

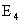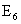Следовательно, m=3. Тогда .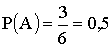

ПРИМЕР 13.2.17. Набирая номер телефона, абонент забыл последние три цифры и помнит лишь то, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.

Решение: Событие A — набраны нужные цифры.

n — общее число элементарных исходов опыта равно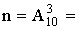

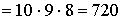
m=1, так как единственная комбинация цифр благоприятствует событию A. Тогда .

.

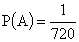ПРИМЕР 13.2.18. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов окажутся 6 отличников.

Решение: Событие A- среди отобранных студентов окажутся 6 отличников. Число n равно числу способов, которыми можно отобрать 9 студентов из 12

.

.

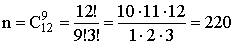Подсчитаем число исходов, благоприятствующих появлению события A. Из 8 отличников 6 можно отобрать 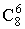способами. Отобрать нужно 9 человек, остальных 3 отбираем среди неотличников. Их всего 12-8=4. Троих студентов-неотличников из четырех можно отобрать 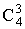способами. По теореме умножения комбинаторики 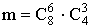. Тогда,

.

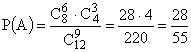Примеры и задачи для самостоятельного решения

Решить задачу, используя формулу классической вероятности

13.2.2.1. В урне белых, черных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар – белый.

Отв.:a/(a+b)

13.2.2.2. Брошены две игральные кости. Найти вероятность того, что сумма очков четная, причем на грани хотя бы одной из костей появится шестерка.

Отв.:5/36

13.2.2.3. В ящике 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

Отв.:0,1

13.2.2.4. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь окрашенных граней: а) одну; б) две; в) три.

Отв.:а)0,384; б)0,096; в)0,008

13.2.2.5. Из тщательно перемешанного полного набора 28 костей домино наудачу извлечена кость. Найти вероятность того, что вторую наудачу извлеченную кость можно приставить к первой, если первая кость: а) оказалась дублем; б) не есть дубль.

Отв.: а) 2/9; б) 4/9

13.2.2.6. Задумано двузначное число. Найти вероятность того, что задуманным числом окажется: а) случайно названное число; б) случайно названное число, цифры которого различны.

Отв.:а) 1/90;б) 1/81

13.2.2.7. Из пяти букв разрезной азбуки составлено слово «ягуар». Ребенок не умеющий читать, рассыпал карточки с буквами и затем собрал в произвольном порядке. Найти вероятность того, что у него снова получится слово «ягуар».

Отв.: 1/120

13.2.2.8. В условиях предыдущей задачи найти вероятность, если ребенок играл со словами: а) молоко; б) шалаш.

Отв.: а)1/120; б)1/30

13.2.2.9. В замке на общей оси пять дисков. Каждый диск разделен на шесть секторов, на которых написаны различные буквы. Замок открывается только в том случае, если каждый диск занимает одно определенное положение относительно корпуса замка. Найти вероятность того, что при произвольной установке дисков замок можно будет открыть.

Отв.: 1/7776

13.2.2.10. В мастерскую для ремонта поступили 10 часов. Известно, что 6 штук из них нуждаются в общей чистке механизма. Мастер берет первые попавшиеся 5 часов. Определить вероятность того, что двое из этих часов нуждаются в общей чистке механизма.

Отв.: 5/21

13.2.2.11. Из партии, в которой 31 деталь без дефектов и 6 с дефектами, берут наудачу 3 детали. Чему равна вероятность в следующих случаях: а) все три детали без дефектов; б) по крайней мере, одна деталь без дефектов?

Отв.:a)0,579; б)0,9973

13.2.2.12. Восемь различных книг расставляются наудачу на одной полке. Найти вероятность того, что две определенные книги окажутся поставленными рядом.

Отв.: 1/4

13.2.2.13. Библиотечка состоит из десяти различных книг, причем пять книг стоят по 4 рубля каждая, три книги – по одному рублю и две книги – по 3 рубля. Найти вероятность того, что взятые наудачу две книги стоят 5 рублей.

Отв.:1/3

13.2.2.14. Найти вероятность выигрышных комбинаций в популярной спортивной лотерее «5 из 36».

Отв.: 1/376992; 155/376992; 775/62832

13.2.2.15. Найти вероятность того, что наудачу выбранное двузначное число делится на 8.

Отв.:11/90

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >