Разложим в ряд Маклорена функцию
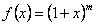,(12.1.60)
где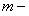 
произвольное постоянное число. К разложению данной функции в ряд подойдем иначе в силу трудности оценки остаточного члена.
Заметим, что функция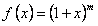 
удовлетворяет дифференциальному уравнению
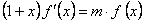(12.1.61)
и условию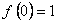 
. Найдем степенной ряд, сумма которого 
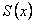удовлетворяет уравнению (12.1.61) и условию 
.
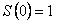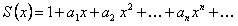(12.1.62)
Подставим ряд (12.62) в уравнение (12.61), получим
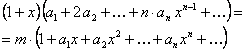
или
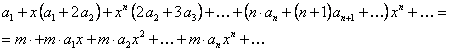
Приравнивая коэффициенты при одинаковых степенях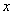 
, учитывая 
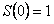получим
.
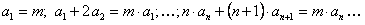Отсюда для коэффициентов ряда получаем выражение
(12.1.63)
Полученные коэффициенты (12.1.63), которые называются биномиальными, подставим в (12.1.62), получим
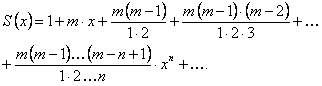(12.1.64)
Полученный ряд (12.1.64) называется биномиальным рядом.
Если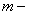 
целое положительное число, то, начиная с члена, содержащего 
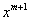, все коэффициенты равны нулю, и ряд превращается в многочлен. При 
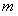дробном или при m целом отрицательном имеем ряд (12.1.64).
Определим радиус сходимости ряда (12.1.64):
.
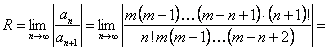
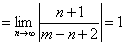Следовательно, в интервале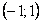 
ряд сходится и представляет функцию 
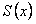, удовлетворяющую дифференциальному уравнению (12.1.61) и начальному условию 
.
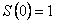Так как дифференциальному уравнению (12.1.61) и условию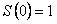 
удовлетворяет единственная функция, то, следовательно, сумма ряда (12.1.64) тождественно равна функции 
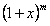, мы получаем разложение
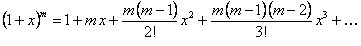(12.1.65)
Частные случаи биномиального ряда.
При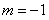 
получаем.
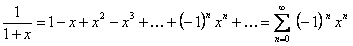. (12.1.66)
При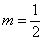 
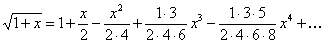(12.1.67)
При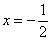 
имеем
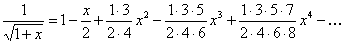(12.1.68)
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
