Вычислениями значений функций приложения теории рядов далеко не исчерпываются. При помощи рядов можно вычислять определенные интегралы.
К вычислениям определенных интегралов с помощью рядов прибегают в том случае, когда интегралы не выражаются в конечном виде через элементарные функции.
ПРИМЕР 12.1.23 Вычислить интеграл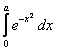 
.
Среди элементарных функций нет такой, производная которой равнялась бы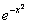 
. Вычислим этот интеграл разложением подынтегральной функции в степенной ряд. Заменяя в формуле (12.1.57) 
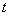на 
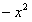, получим
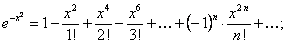поэтому
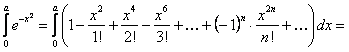
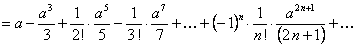(12.1.76)
Подставляя в полученный ряд вместо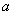 
те или иные значения, можно вычислить интеграл при любом верхнем пределе.
Пусть требуется вычислить этот интеграл с тремя верными десятичными знаками, когда верхний предел интегрирования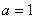 
. Полагая в (12.1.76) 
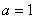, получим
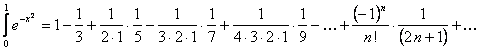(12.1.77)
Поскольку вычисление следует производить с тремя верными десятичными знаками, то погрешность не должна превышать 
. В правой части равенства стоит знакочередующийся ряд. Поэтому в разложении необходимо сохранить столько членов, чтобы первый из отброшенных был меньше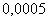 
. Вычислим члены нашего ряда, начиная с четвертого:
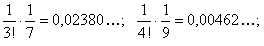
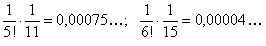
Значит, если мы сохраним в ряде только первые шесть членов, то погрешность при этом будет по абсолютной величине меньше первого отброшенного, то есть седьмого (меньше, чем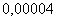 
). Окончательно получаем
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
