Признак Даламбера. Если в ряде с положительными членами
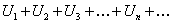(12.1.9)
отношение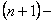 
го члена к 
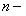му при 
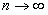имеет (конечный) предел l, то есть
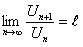,(12.1.10)
1) при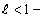 
ряд сходится;
2) при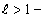 
ряд расходится;
3) при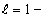 
этот признак не решает вопроса о сходимости и расходимости.
Доказательство. 1. Пусть для исследуемого ряда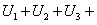 
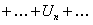
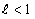. Рассмотрим число 
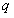, удовлетворяющее соотношению 
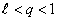. Тогда, начиная с некоторого номера 
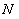из определения предела, для всех 
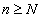, выполняется неравенство
.
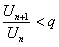Действительно, так как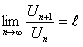 
, то разность между величиной 
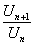и числом 
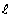может быть сделана по абсолютной величине меньше любого положительного числа, в частности, меньше, чем 
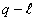, то есть
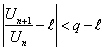.(12.1.11)
Неравенство (3) может быть записано в виде
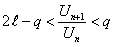.(12.1.12)
Запишем правую часть неравенства (12.1.12) для различных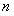 
, начиная с номера 
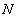, получим
;
;
.
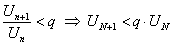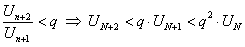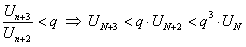Рассмотрим два ряда
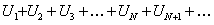(12.1.13)
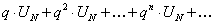(12.1.14)
Ряд (12.1.14) есть ряд геометрической прогрессии со знаменателем q,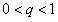 
. Следовательно, он сходится. Так как члены ряда (12.1.13) начиная с 
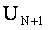меньше соответствующих членов ряда (12.1.14), то на основании признака сравнения ряд (12.1.13) сходится.
2. Пусть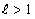 
. Тогда из равенства 
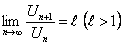следует, что, начиная с некоторого номера 
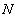(то есть для 
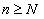) будет иметь место неравенство 
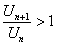или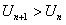 
, а это означает, что члены ряда возрастают и общий член ряда не стремится к нулю при 
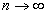, то есть нарушается необходимый признак сходимости, что приводит к расходимости исследуемого ряда.
ПРИМЕР 12.1.4 Исследовать сходимость числового ряда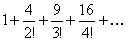 
Решение. Запишем n-й член ряда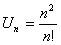 
. Проверим необходимый признак сходимости
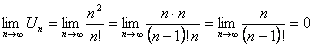
Необходимый признак выполняется, ряд может сходиться. Для установления сходимости применим признак Даламбера, для чего запишем член
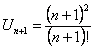. Тогда
.
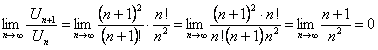Значит, в данном случае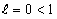 
и ряд сходится.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
