Ряды по степеням (x-x0)
Функциональный ряд вида
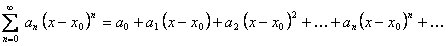 (12.1.46)
(12.1.46)
называется степенным рядом по степеням разности 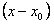 . Нетрудно заметить, что при
. Нетрудно заметить, что при 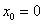 из ряда (1) получается известный степенной ряд
из ряда (1) получается известный степенной ряд 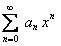 . Следовательно, ряд
. Следовательно, ряд 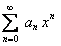 является частным случаем ряда (12.1.46).
является частным случаем ряда (12.1.46).
Для определения интервала сходимости ряда (12.1.46) сделаем в нем замену: 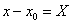 . Тогда ряд (12.1.46) примет вид
. Тогда ряд (12.1.46) примет вид
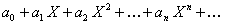 . (12.1.47)
. (12.1.47)
Ряд (12.1.47) по степеням 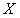 . Пусть интервал сходимости ряда (12.1.47)
. Пусть интервал сходимости ряда (12.1.47) 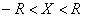 .
.
Отсюда следует, что ряд (12.1.46) будет сходиться при значениях 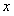 , удовлетворяющих неравенству
, удовлетворяющих неравенству 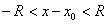 или
или 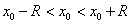 и расходиться при
и расходиться при 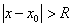 . Следовательно, интервалом сходимости данного ряда будет интервал
. Следовательно, интервалом сходимости данного ряда будет интервал 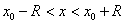 с центром в точке
с центром в точке 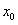 .
.
Замечание. Все сказанное о степенных рядах по степеням 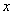 остается справедливым и для степенных рядов по степеням разности
остается справедливым и для степенных рядов по степеням разности 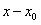 в соответствующих интервалах сходимости.
в соответствующих интервалах сходимости.
ПРИМЕР 12.1.18 Найти радиус сходимости ряда 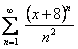 .
.
Решение. Найдем радиус сходимости

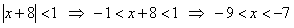
При 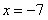 получим числовой ряд
получим числовой ряд 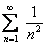 , который сходится, так как является обобщенным гармоническим рядом с
, который сходится, так как является обобщенным гармоническим рядом с 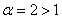 .
.
При 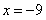 получим числовой знакочередующийся ряд
получим числовой знакочередующийся ряд 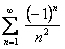 , для которого выполняются условия теоремы Лейбница, и он сходится. Следовательно, областью сходимости данного ряда является отрезок
, для которого выполняются условия теоремы Лейбница, и он сходится. Следовательно, областью сходимости данного ряда является отрезок 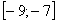 .
.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >