Пусть задача сводится к случайному бросанию точки на ограниченную фигуру 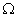 (отрезок прямой [a,b] , часть плоскости D, тело в пространстве V) меры
(отрезок прямой [a,b] , часть плоскости D, тело в пространстве V) меры 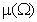 .
.
Пусть имеет место «схема случаев». Классическое определение к данному испытанию неприменимо, так как число исходов бесконечно (оно равно числу точек фигуры 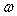 ). В этом случае применяется геометрическое определение вероятности.
). В этом случае применяется геометрическое определение вероятности.
Пусть событие А состоит в том, что случайная точка попадает в область 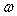 , являющуюся частью фигуры
, являющуюся частью фигуры 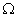 и имеющую меру
и имеющую меру 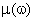 . Тогда вероятность события определяется по формуле
. Тогда вероятность события определяется по формуле
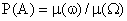 (13.1.9)
(13.1.9)
Здесь фигура 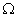 есть множество возможных, а фигура
есть множество возможных, а фигура 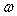 — множество благоприятных исходов испытания. Следовательно, формула (13.1.9) есть обобщение формулы (13.1.2) на случай испытаний с бесконечным числом исходов.
— множество благоприятных исходов испытания. Следовательно, формула (13.1.9) есть обобщение формулы (13.1.2) на случай испытаний с бесконечным числом исходов.
ПРИМЕР 13.1.9 (задача Бюффона) Плоскость расчерчена параллельными прямыми, расстояние между которыми равно 2а. На плоскость наудачу брошена игла длиной 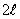
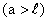 .Найти вероятность того, что игла пересечет какую-нибудь прямую.
.Найти вероятность того, что игла пересечет какую-нибудь прямую.
Решение. Пусть U – расстояние от центра иглы до ближайшей прямой, а 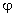 — угол, составленный иглой с этой прямой. Пара чисел
— угол, составленный иглой с этой прямой. Пара чисел 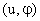 задает положение иглы с точностью до выбора конкретной прямой. Поскольку нас интересует взаимное расположение иглы с ближайшей прямой, то в качестве
задает положение иглы с точностью до выбора конкретной прямой. Поскольку нас интересует взаимное расположение иглы с ближайшей прямой, то в качестве  возьмем прямоугольник:
возьмем прямоугольник:
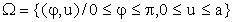
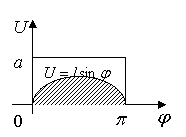
Пересечение иглы с прямой происходит только в том случае, когда 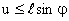 (см. рис. 13.1.1)
(см. рис. 13.1.1)
 ,
, 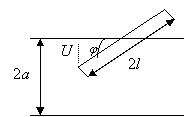
рис. 13.1.1
Множество точек фигуры  , благоприятных для наступления интересующего нас события А, описывается условием
, благоприятных для наступления интересующего нас события А, описывается условием
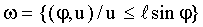
Имеем:
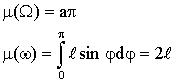
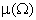 — площадь прямоугольника,
— площадь прямоугольника, 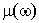 — площадь заштрихованной фигуры.
— площадь заштрихованной фигуры.
По формуле (13.1.9) получим 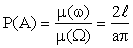
Соответствие рассмотренной математической модели опыту можно проверить экспериментально.
Пусть игла брошена n раз, m раз при этом пересекла линию.
Тогда 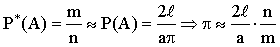
Тем самым можно экспериментально найти оценку числа 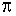 . Результаты такой проверки приведены в таблице:
. Результаты такой проверки приведены в таблице:
| Испытатель |  |
m | n | Оценка числа  |
| Рейн, 1925г. | 0,5419 | 2520 | 850 | 3,1795 |
| Вольф, 1950г. | 0,8 | 5000 | 2532 | 3,1596 |
Онлайн помощь по математике
Лекции по высшей математике
Примеры решения задач