Законом распределения дискретной двумерной случайной величины называют перечень возможных значений этой величины, т. е. пар чисел 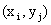и их вероятностей 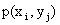(i=1,2, … ,n; j=1,2, … ,m). Обычно закон распределения задают в виде таблицы с двойным входом (см. табл.1), называемой матрицей распределения.

Первая строка таблицы содержит все возможные значения составляющей X, а первый столбец – все возможные значения составляющей Y. В клетке, стоящей на пересечении столбца и строки, указана вероятность 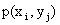того, что двумерная случайная величина примет значение .

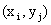Так как события 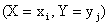(i=1,2, … ,n; j=1,2, … ,m) образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы 13.1, равна единице.

Таблица 13.1

Y\X			…		…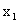
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

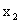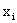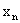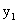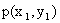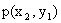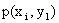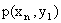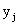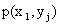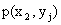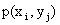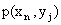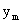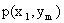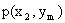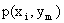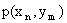Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события 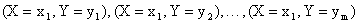несовместны, поэтому вероятность 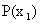того, что X примет значение 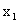, по теореме сложения такова:

.

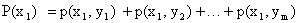Таким образом, вероятность того, что X примет значение 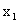, равна сумме вероятностей “столбца 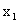”. В общем случае для того, чтобы найти вероятность 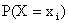, надо просуммировать вероятности столбца 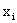. Аналогично сложив вероятности “строки 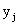“, получим вероятность .

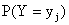ПРИМЕР 13.1.50 Найти законы распределения составляющих двумерной случайной величины, заданной законом распределения (табл.13.2).

Y\X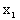
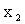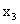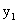	0,10	0,15	0,25
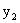	0,12	0,20	0,18

Решение. Сложив вероятности по столбцам, получим вероятности возможных значений X: .
Напишем закон распределения составляющей X: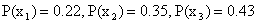

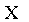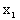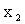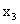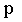	0,22	0,35	0,43

Контроль: 0,22+0,35+0,43=1.

Сложив вероятности по строкам, получим вероятности возможных значений Y: .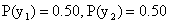

Напишем закон распределения составляющей Y:

Y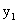
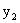P	0,50	0,50

Контроль: 0,50+0,50=1.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >