Неравенство Чебышева справедливо как для дискретных, так и непрерывных случайных величин. Для простоты докажем это неравенство для дискретных величин.

Рассмотрим дискретную случайную величину X, заданную таблицей распределения:

			…
			…

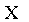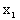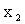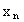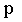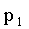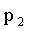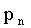Оценим вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа 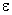. Если 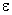достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. П.Л. Чебышев доказал неравенство, позволяющее дать интересующую нас оценку.

Помощь с решением

Неравенство Чебышева. Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше положительного числа 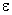, не меньше, чем :

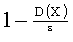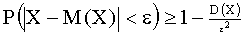
Доказательство. Так как события, состоящие в осуществлении неравенства
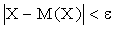и 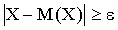, противоположны, то сумма их вероятностей равна единице, т.е.

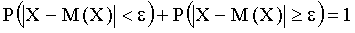
Отсюда интересующая нас вероятность 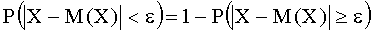. (13.1.35)

Таким образом, задача сводится к вычислению вероятности

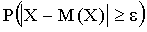
Выражение для дисперсии случайной величины X:

.

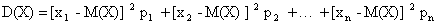Очевидно, все слагаемые этой суммы неотрицательны.

Отбросим те слагаемые, у которых 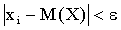(для оставшихся слагаемых 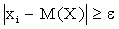), вследствие чего сумма может только уменьшиться. Условимся считать для определенности, что отброшено k первых слагаемых (не нарушая общности, можно считать, что в таблице распределения возможные значения занумерованы именно в таком порядке). Таким образом,

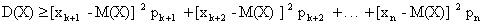
Заметим, что обе части неравенства 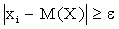( j=k+1,k+2,…,n) положительны, поэтому, возведя их в квадрат, получим равносильное неравенство .

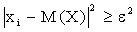Воспользуемся этим замечанием и, заменяя в оставшейся сумме каждый из множителей 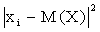числом 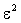(при этом неравенство может лишь усилиться), получим

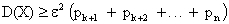. (13.1.36)

По теореме сложения сумма вероятностей 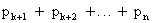есть вероятность того, что X примет одно, безразлично какое, из значений 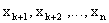, а при любом из них отклонение удовлетворяет неравенству .

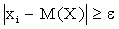Отсюда следует, что сумма 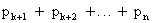выражает вероятность

.

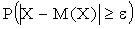Это соображение позволяет переписать неравенство (1.36) так:,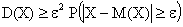

или

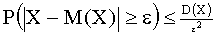(13.1.37)

Подставляя (13.1.37) в (13.1.35), окончательно получим

,

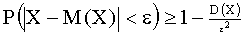что и требовалось доказать.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >