Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
Пусть случайная величина Х может принимать только значения 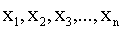 , вероятности которых соответственно равны
, вероятности которых соответственно равны 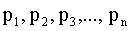 .
.
Тогда математическое ожидание М(X) случайной величины Х определяется равенством
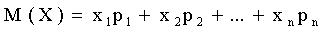 ,
,
Если дискретная случайная величина Х принимает счетное множество возможных значений, то
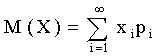 ,
,
причем математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Замечание. Из определения следует, что математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем будет показано, что математическое ожидание непрерывной случайной величины также есть постоянная величина.
ПРИМЕР 13.1.29 Найти математическое ожидание случайной величины X, зная закон ее распределения:
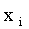 |
0 | 5 | 10 | 15 |
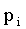 |
0,216 | 0,432 | 0,288 | 0,064 |
Решение. Искомое математическое ожидание равно сумме произведений всех возможных значений случайной величины на их вероятности:
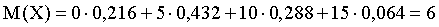 .
.
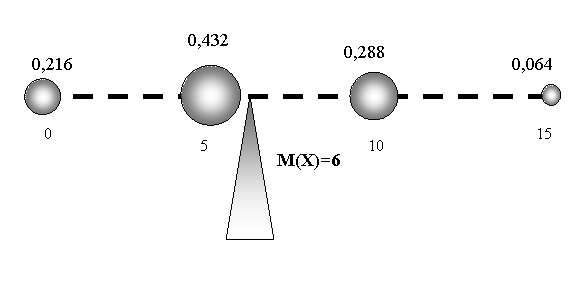
На рисунке представлена механическая интерпретация М(X) как абсциссы центра тяжести системы материальных точек, абсциссы которых равны возможным значениям случайной величины, а массы — их вероятностям.
ПРИМЕР 13.1.30 Найти математическое ожидание числа появлений события А в одном испытании, если вероятность события А равна р.
Решение. Случайная величина Х — число появлений события А в одном испытании — может принимать только два значения 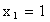 , (событие А наступило) с вероятностью р и
, (событие А наступило) с вероятностью р и 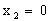 , (событие А не наступило) с вероятностью q=1-p. Искомое математическое ожидание
, (событие А не наступило) с вероятностью q=1-p. Искомое математическое ожидание
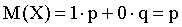 ,
,
Итак, математическое ожидание числа появлений события в одном испытании равно вероятности этого события.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >