Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины X, которое описывается плотностью ,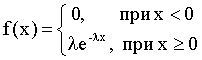

где 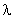— постоянная положительная величина.

Таким образом, показательное распределение определяется только одним параметром.

Найдем функцию распределения показательного закона:
.

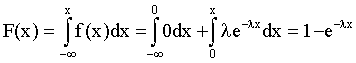Следовательно,
.

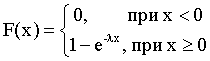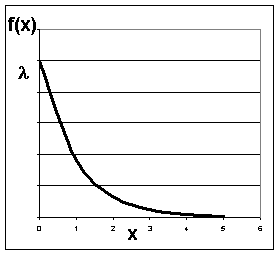
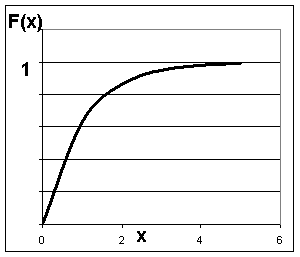
Графики плотности и функции распределения показательного закона изображены на рис.13.1.22, 13.1.23.

Рис.13.1.22	Рис.13.1.23

Найдем вероятность попадания в интервал (a;b) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения F(x).

Для этого используем формулу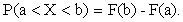

Учитывая, что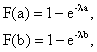

получим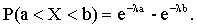

ПРИМЕР 13.1.47 Непрерывная случайная величина Х распределена по показательному закону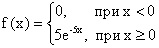

Найти вероятность того, что в результате испытания Х попадет в интервал (0,6;2).

Решение. По условию, 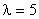. Тогда
.

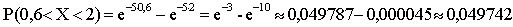Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >