При применении локальной теоремы Муавра – Лапласа можно заметить, что асимптотическое представление вероятности 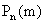посредством функции 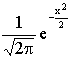действует тем хуже, чем больше вероятность p отличается от половины, то есть чем меньше значения p или q приходится рассматривать, и это представление отказывается служить при 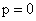, 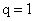и при , .

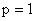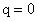Однако значительный круг задач связан с необходимостью вычисления вероятностей 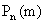именно при малых значениях p.

Для того, чтобы в этом случае теорема Муавра – Лапласа дала результаты с незначительной ошибкой, необходимо, чтобы число испытаний было очень велико. Возникает, таким образом, задача разыскания асимптотической формулы, специально приспособленной для случая малых p. Такая формула была найдена Пуассоном.

ТЕОРЕМА 13.1.9. (Пуассона). Есл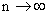и и 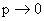так, ч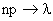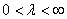то (), то

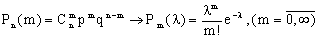(13.1.33)

(для функции 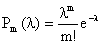имеется таблица).

Доказательство:

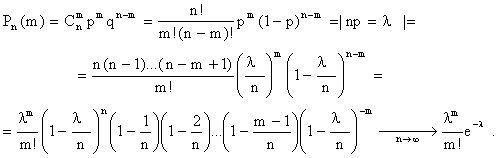
Таким образом, при больших n и малых p справедлива формула (обычно p<0.1; )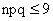

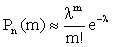, где 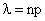. (13.1.34)

ПРИМЕР 13.1.22 Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0.001. Найти вероятность того, что на базу прибудут не более 2 негодных изделий.

Решение. ,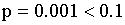

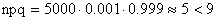
Значит, можно использовать формулу Пуассона ;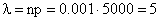

; ; ;

.

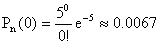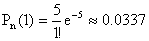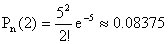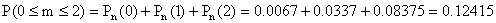Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >