Пусть (X,Y) – непрерывная двумерная случайная величина.
Условной плотностью 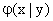 распределения составляющих X при данном значении Y = y называют отношение плотности совместного распределения f(x,y) системы (X,Y) к плотности распределения
распределения составляющих X при данном значении Y = y называют отношение плотности совместного распределения f(x,y) системы (X,Y) к плотности распределения 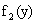 составляющей Y:
составляющей Y:
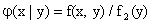 . (13.1.46)
. (13.1.46)
Подчеркнем, что отличие условной плотности 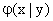 от безусловной плотности
от безусловной плотности 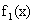 состоит в том, что функция
состоит в том, что функция 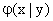 дает распределение X при условии, что составляющая Y приняла значение Y = y; функция же
дает распределение X при условии, что составляющая Y приняла значение Y = y; функция же 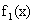 дает распределение X независимо от того, какие из возможных значений приняла составляющая Y.
дает распределение X независимо от того, какие из возможных значений приняла составляющая Y.
Аналогично определяется условная плотность составляющей Y при заданном значении X = x:
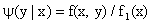 . (13.1.47)
. (13.1.47)
Если известна плотность совместного распределения f(x, y), то условные плотности составляющих могут быть найдены в силу (13.1.46) и (13.1.47) по формулам
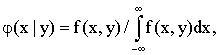 (13.1.48)
(13.1.48)
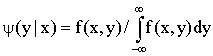 . (13.1.49)
. (13.1.49)
Запишем формулы (13.1.46) и (13.1.47) в виде
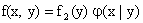 ,
, 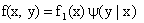 .
.
Отсюда заключаем: умножая закон распределения одной из составляющих на условный закон распределения другой составляющей, найдем закон распределения системы случайных величин.
Как и любая плотность распределения, условные плотности обладают следующими свойствами:
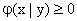 ,
, 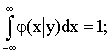 ,
,
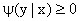 ,
, 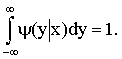 ,
,
ПРИМЕР 13.1.57 Двумерная случайная величина (X,Y) задана плотностью совместного распределения

Найти условные законы распределения вероятностей составляющих.
Решение. Найдем условную плотность составляющей X при 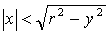 ,
,
по формуле (13.1.48):
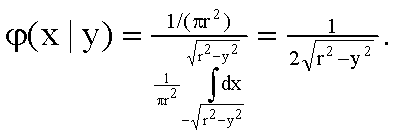
Так как f(x, y) = 0 при 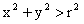 , то
, то 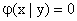 при
при 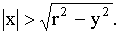 .
.
Пользуясь формулой (13.1.49), аналогично найдем условную плотность составляющей Y:
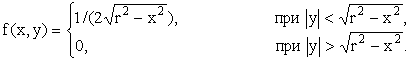
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >