Пусть F(х) — функция распределения непрерывной случайной величины X. По определению плотности распределения

,

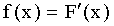или в иной форме

.

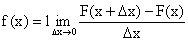Как уже известно, разность 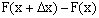определяет вероятность того, что Х примет значение, принадлежащее интервалу 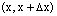. Таким образом, предел отношения вероятности того, что непрерывная случайная величина примет значение, принадлежащее интервалу 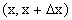, к длине этого интервала при 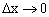равен значению плотности распределения в точке х.

Итак, функция f(х) определяет плотность распределения вероятности для каждой точки х.

Как известно, приращение функции приближенно равно дифференциалу функции, т.е.

,

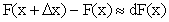или

.

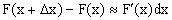Так как

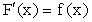
и

,

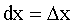то

.

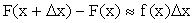Вероятностный смысл этого равенства следующий: вероятность того, что случайная величина примет значение, принадлежащее интервалу 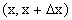, приближенно равна (с точностью до бесконечно малых высшего порядка относительно 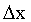) произведению плотности вероятности в точке х на длину интервала .

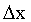Геометрически этот результат можно истолковать так: вероятность того, что случайная величина примет значение, принадлежащее интервалу 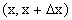, приближенно равна площади прямоугольника с основанием 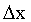и высотой .

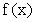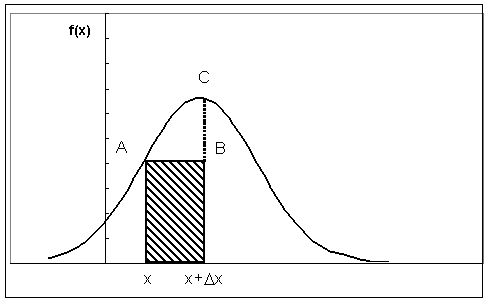
На рис.13.1.10 видно, что площадь заштрихованного прямоугольника, равная произведению 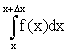, лишь приближенно равна площади криволинейной трапеции (истинной вероятности, определяемой определенным интегралом 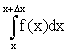). Допущенная при этом погрешность равна площади криволинейного треугольника ABC.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >