Вернемся к схеме независимых испытаний Бернулли с постоянными условиями. Легко убедиться, что точное вычисление вероятностей для больших значений n по формуле Бернулли через факториалы достаточно трудоемко.

В ряде случаев можно вычисления упростить, если воспользоваться таблицами факториалов или формулой Стирлинга: 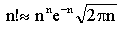, т.е. 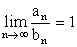. Однако и этот путь остается громоздким и не всегда обеспечивает требуемую точность. Возникла необходимость в асимптотических формулах, позволяющих с достаточной степенью точности определять эти вероятности.

Функцию 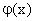называют асимптотическим приближением функции 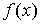, если .

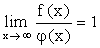Впервые формула такого рода была найдена Муавром в 1730 г. для частного случая схемы Бернулли при 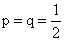, а затем обобщена Лапласом в 1783 г. на случай произвольного p, отличного от 0 и 1. Поэтому формулу, о которой идет речь, называют теоремой Муавра – Лапласа. Теоремы Муавра – Лапласа применяются для приближенного вычисления вероятностей

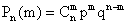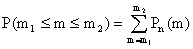и в схеме Бернулли при больших .

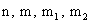ТЕОРЕМА 13.1.7. (Локальная теорема Муавра – Лапласа). Если вероятность наступления события A в n независимых испытаниях постоянна и равна p , то вероятность 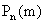того, что в этих испытаниях событие A наступит ровно m раз, приближенно равна (тем точнее, чем больше )

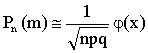, (13.1.31)

где p — вероятность наступления события A в каждом испытании,

; ; .

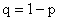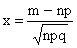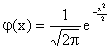ТЕОРЕМА 13.1.8. (Интегральная теорема Муавра – Лапласа) Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 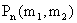того, что в испытаниях событие A наступит от 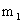до 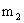раз, приближенно равна

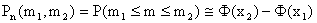, (13.1.32)

где 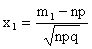; ; 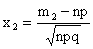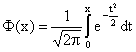— функция Лапласа.

Для функци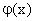и и 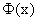имеются таблицы для .

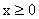Для отрицательных аргументов 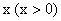значения этих функций находят с учетом того, что 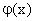— четная, а 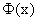— нечетная функции. Приближенные формулы (13.1.31, 13.1.32) применяют в случаях, когда p и q не малы, а .

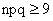ПРИМЕР 1.21 Вероятность наступления события A в каждом из 900 независимых испытаний равна 0,8. Найти вероятность того, что событие A произойдет: 1). 750 раз; 2) от 710 до 740 раз.

Решение. Так как 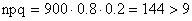, то формулы (13.1.31, 13.1.32) можно использовать.

1) ;

;

;

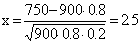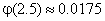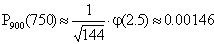2) ;

;

,

,

.

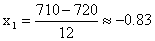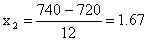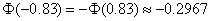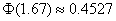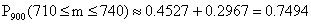Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >