Пусть дана квадратная матрица 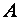 порядка
порядка 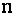 .
.

ОПРЕДЕЛЕНИЕ 1.13
Квадратная матрица 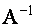 порядка
порядка 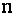 называется обратной матрицей для данной матрицы
называется обратной матрицей для данной матрицы 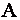 , если
, если
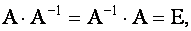 |
(1.16) |
где 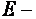 единичная матрица.
единичная матрица.
Обозначим через 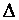 определитель матрицы
определитель матрицы 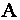 и вычислим его. Тогда, если
и вычислим его. Тогда, если 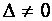 , то матрицу
, то матрицу 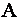 называют неособенной (невырожденной) матрицей, если же
называют неособенной (невырожденной) матрицей, если же 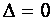 , то особенной (вырожденной) матрицей.
, то особенной (вырожденной) матрицей.
ТЕОРЕМА 1.3
Всякая неособенная матрица 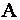 имеет обратную матрицу
имеет обратную матрицу 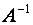 , определяемую формулой
, определяемую формулой
 , , |
(1.17) |
где 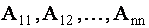 есть алгебраические дополнения соответствующих элементов
есть алгебраические дополнения соответствующих элементов 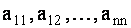 матрицы
матрицы 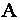 .
.
Доказательство. Покажем, что 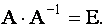 Действительно,
Действительно,
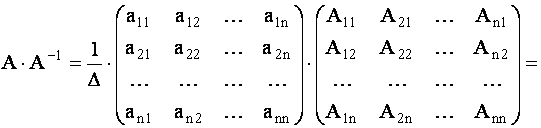

Согласно обобщению теоремы 1.1 о разложении определителя по элементам любой строки все элементы, расположенные на главной диагонали предыдущей матрицы, равны 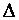 , а оставшиеся элементы, согласно обобщению теоремы 1.2, равны нулю. Тогда
, а оставшиеся элементы, согласно обобщению теоремы 1.2, равны нулю. Тогда

Аналогично доказывается, что 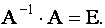
ПРИМЕР 1.1.12
Найти матрицу 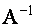 , если
, если 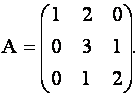
Решение. Выясним, является ли матрица 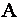 невырожденной
невырожденной
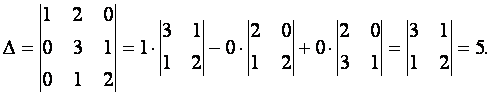
Так как определитель 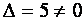 , то матрица
, то матрица 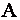 невырожденная и имеет обратную матрицу
невырожденная и имеет обратную матрицу 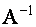 .
.
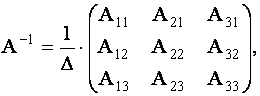 где
где
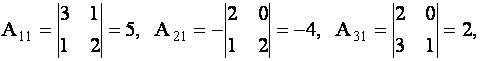
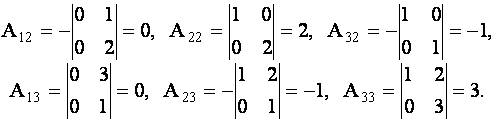
Подставляя найденные числа в формулу для 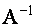 , получим
, получим
