Основные понятия
Определители и матрицы широко применяются при решении систем линейных уравнений, т.е. систем, содержащих 
уравнений первой степени относительно 
неизвестных 
.
В наиболее общем виде такие системы записываются в форме
 |
(1.18) |
Числа 
называются коэффициентами системы или коэффициентами при неизвестных.
Первый индекс у коэффициентов системы указывает на номер уравнения, второй на номер неизвестного, при котором записан этот коэффициент. Числа 
называются свободными членами. Если все свободные члены равны нулю, то система называется однородной, если же, хотя бы одно из них отлично от нуля, то неоднородной.
ОПРЕДЕЛЕНИЕ 1.14
Решением системы (1.18) называется любая совокупность чисел , подстановка которой в (1.18) обращает каждое уравнение этой системы в верное числовое равенство.
Система, имеющая хотя бы одно решение, называется совместной, имеющая только одно решение определенной, имеющая более одного решения — неопределенной, не имеющая ни одного решения — несовместной.
Решить систему (1.18) — это значит указать все множество ее решений или доказать ее несовместность.
ОПРЕДЕЛЕНИЕ 1.15
Две системы линейных уравнений называются равносильными, если каждое решение второй системы является решением первой и наоборот.
Доказано, что если над системой (1.18) выполнить преобразования:
- переменить местами уравнения;
- умножить обе части любого уравнения системы на любое не равное нулю число;
- прибавить к обеим частям одного из уравнений системы соответствующие части другого уравнения, умноженные на любое действительное число, то система (1.18) переходит в равносильную ей систему. Перечисленные выше преобразования называются элементарными преобразованиями системы. В результате элементарного преобразования может случиться, что в системе появится уравнение, все коэффициенты которого равны нулю. Тогда, если и свободный член этого уравнения равен нулю, то уравнение справедливо при любых
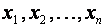и, следовательно, его можно отбросить. Если же свободный член не равен нулю, то это уравнение не удовлетворяется никакими значениями неизвестных, следовательно, полученная система является несовместной. Тогда несовместна и исходная система.